Analisis Diskriminan dengan tidymodels

R Programming
Statistical Machine Learning
tidymodels
Author

Gerry Alfa Dito

Published

April 2, 2024

install.packages("rattle")
install.packages("MVN")
install.packages("heplots")
library(lares)
library(discrim)
library(tidyverse)
library(tidymodels)
library(themis)
library(easystats)
library(SmartEDA)
library(DataExplorer)
library(skimr)
library(ggpubr)
library(workflowsets)

Deskripsi singkat data

Dataset wine berisi hasil analisis kimiawi dari anggur yang ditanam di daerah tertentu di Italia. Tiga jenis anggur diwakili dalam 178 sampel, dengan hasil 13 analisis kimia yang dicatat untuk setiap sampel. Variabel Type telah diubah menjadi variabel kategorik.

data ini bisa diperoleh dari package rattle

Import data di R

data(wine, package='rattle')
df <- wine
rm(wine)
glimpse(df)
Rows: 178
Columns: 14
$ Type            <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ Alcohol         <dbl> 14.23, 13.20, 13.16, 14.37, 13.24, 14.20, 14.39, 14.06…
$ Malic           <dbl> 1.71, 1.78, 2.36, 1.95, 2.59, 1.76, 1.87, 2.15, 1.64, …
$ Ash             <dbl> 2.43, 2.14, 2.67, 2.50, 2.87, 2.45, 2.45, 2.61, 2.17, …
$ Alcalinity      <dbl> 15.6, 11.2, 18.6, 16.8, 21.0, 15.2, 14.6, 17.6, 14.0, …
$ Magnesium       <int> 127, 100, 101, 113, 118, 112, 96, 121, 97, 98, 105, 95…
$ Phenols         <dbl> 2.80, 2.65, 2.80, 3.85, 2.80, 3.27, 2.50, 2.60, 2.80, …
$ Flavanoids      <dbl> 3.06, 2.76, 3.24, 3.49, 2.69, 3.39, 2.52, 2.51, 2.98, …
$ Nonflavanoids   <dbl> 0.28, 0.26, 0.30, 0.24, 0.39, 0.34, 0.30, 0.31, 0.29, …
$ Proanthocyanins <dbl> 2.29, 1.28, 2.81, 2.18, 1.82, 1.97, 1.98, 1.25, 1.98, …
$ Color           <dbl> 5.64, 4.38, 5.68, 7.80, 4.32, 6.75, 5.25, 5.05, 5.20, …
$ Hue             <dbl> 1.04, 1.05, 1.03, 0.86, 1.04, 1.05, 1.02, 1.06, 1.08, …
$ Dilution        <dbl> 3.92, 3.40, 3.17, 3.45, 2.93, 2.85, 3.58, 3.58, 2.85, …
$ Proline         <int> 1065, 1050, 1185, 1480, 735, 1450, 1290, 1295, 1045, 1…

Eksplorasi Data

df %>% 
  skim_without_charts()
Data summary
Name Piped data
Number of rows 178
Number of columns 14
_______________________
Column type frequency:
factor 1
numeric 13
________________________
Group variables None

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
Type 0 1 FALSE 3 2: 71, 1: 59, 3: 48

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100
Alcohol 0 1 13.00 0.81 11.03 12.36 13.05 13.68 14.83
Malic 0 1 2.34 1.12 0.74 1.60 1.87 3.08 5.80
Ash 0 1 2.37 0.27 1.36 2.21 2.36 2.56 3.23
Alcalinity 0 1 19.49 3.34 10.60 17.20 19.50 21.50 30.00
Magnesium 0 1 99.74 14.28 70.00 88.00 98.00 107.00 162.00
Phenols 0 1 2.30 0.63 0.98 1.74 2.36 2.80 3.88
Flavanoids 0 1 2.03 1.00 0.34 1.20 2.13 2.88 5.08
Nonflavanoids 0 1 0.36 0.12 0.13 0.27 0.34 0.44 0.66
Proanthocyanins 0 1 1.59 0.57 0.41 1.25 1.56 1.95 3.58
Color 0 1 5.06 2.32 1.28 3.22 4.69 6.20 13.00
Hue 0 1 0.96 0.23 0.48 0.78 0.96 1.12 1.71
Dilution 0 1 2.61 0.71 1.27 1.94 2.78 3.17 4.00
Proline 0 1 746.89 314.91 278.00 500.50 673.50 985.00 1680.00

Distribusi Variabel Kategorik

df %>% 
  ExpCatViz(clim = 10,
            col = "#107896",
            Page = NULL,
            Flip = TRUE)
[[1]]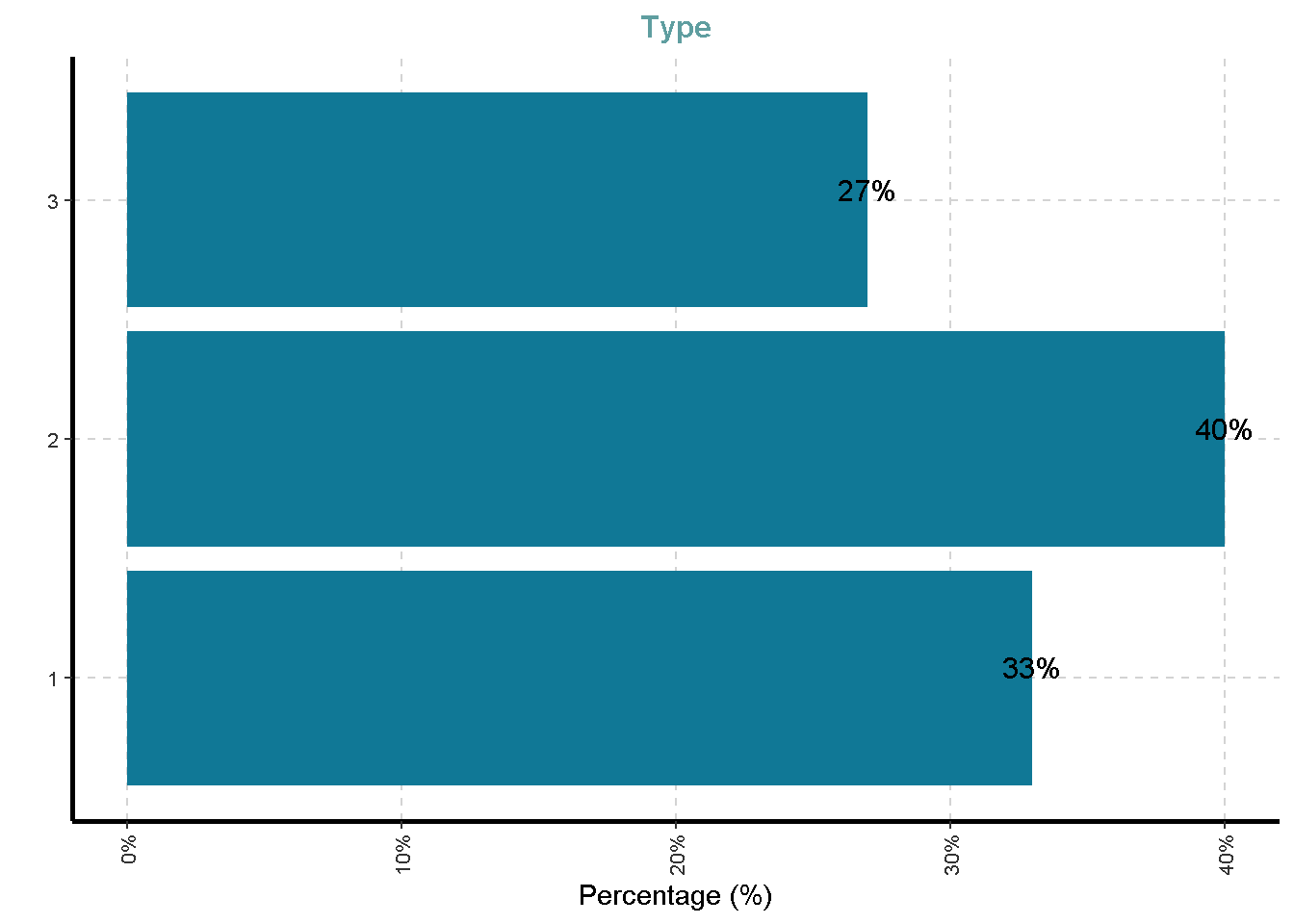

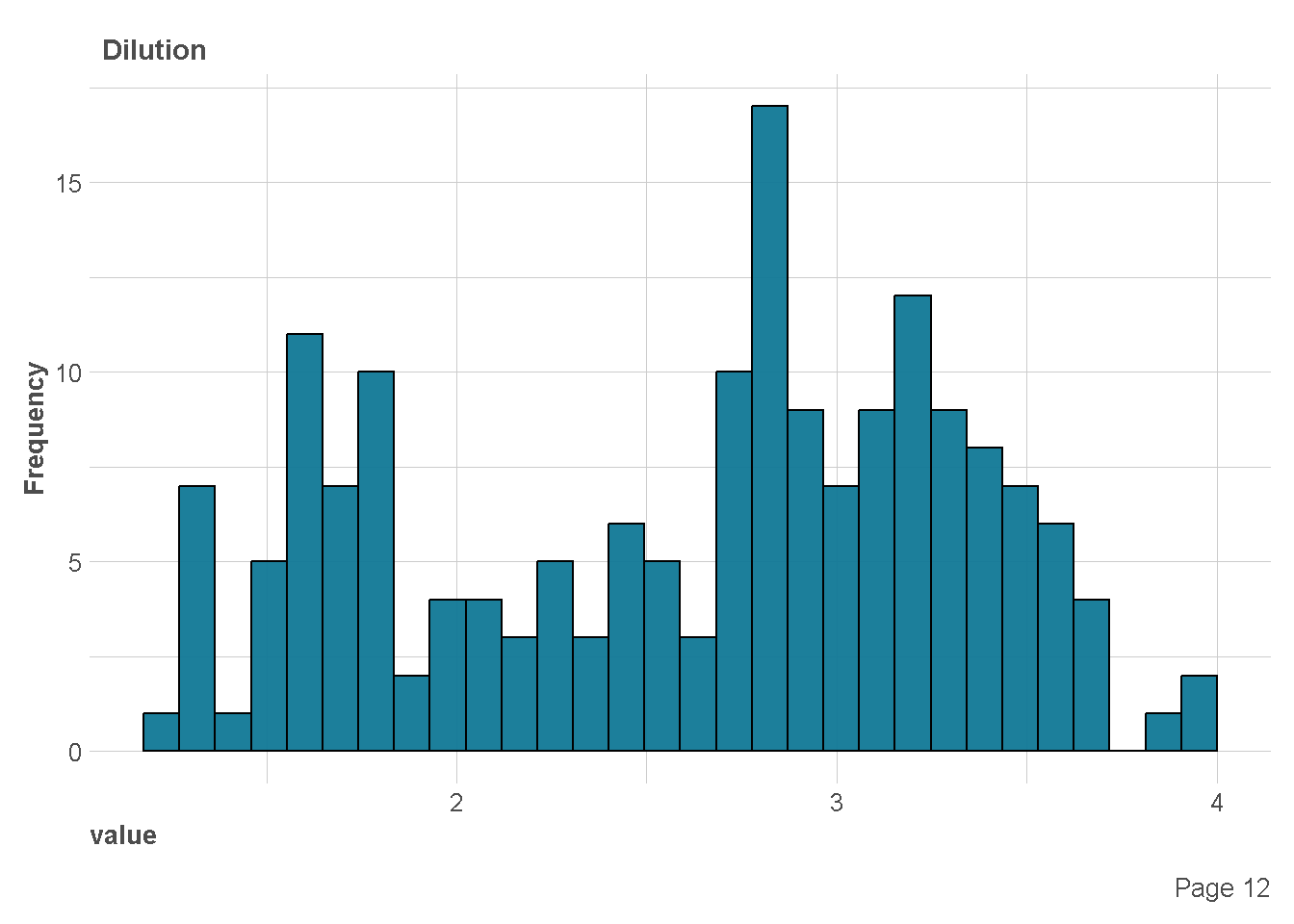
Distribusi Variabel Numerik

df %>% 
  plot_histogram(
             ggtheme = theme_lares(),
             geom_histogram_args = list(bins=30,
                                        col="black",
                                        fill="#107896"),
             ncol = 1,nrow = 1)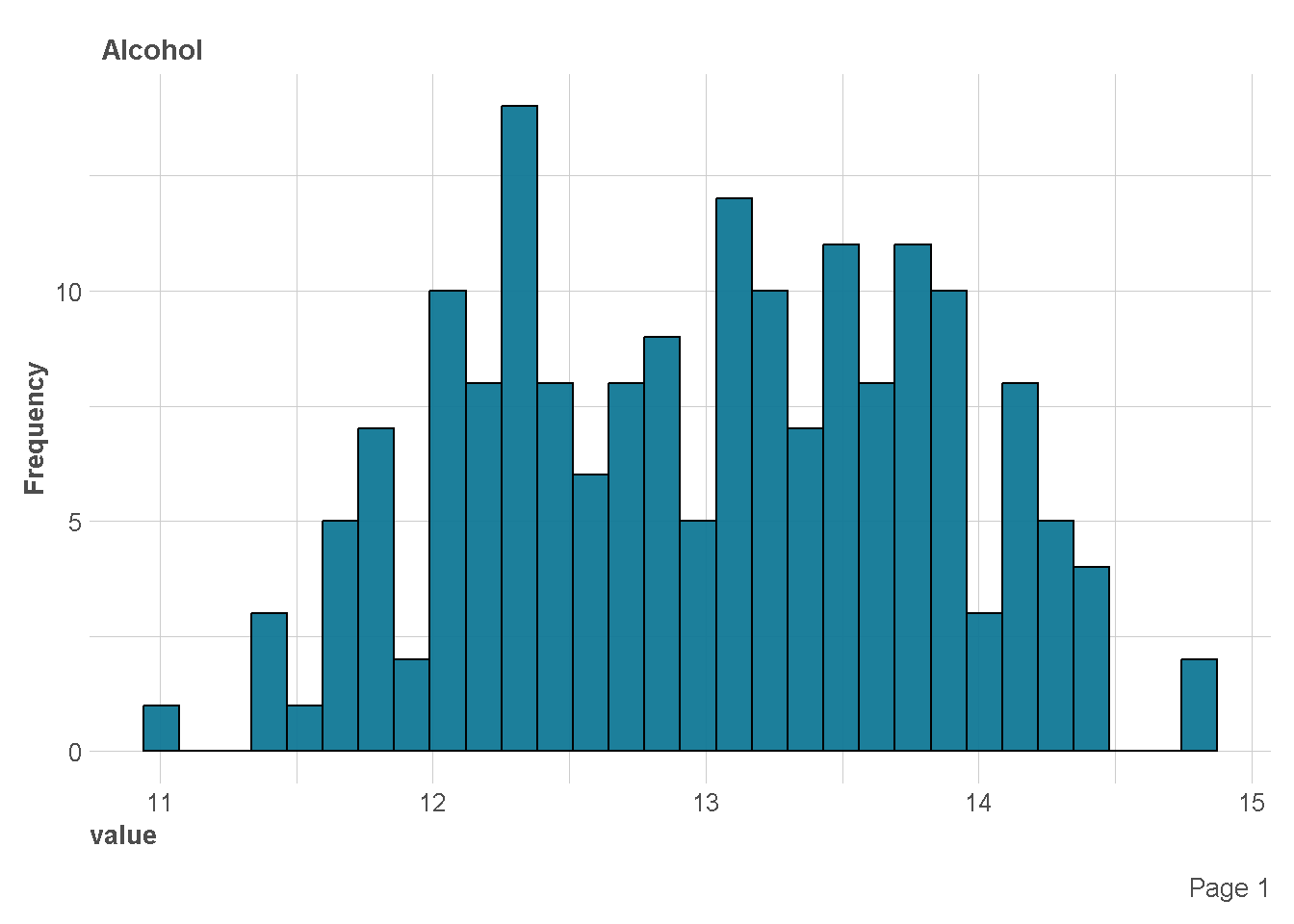

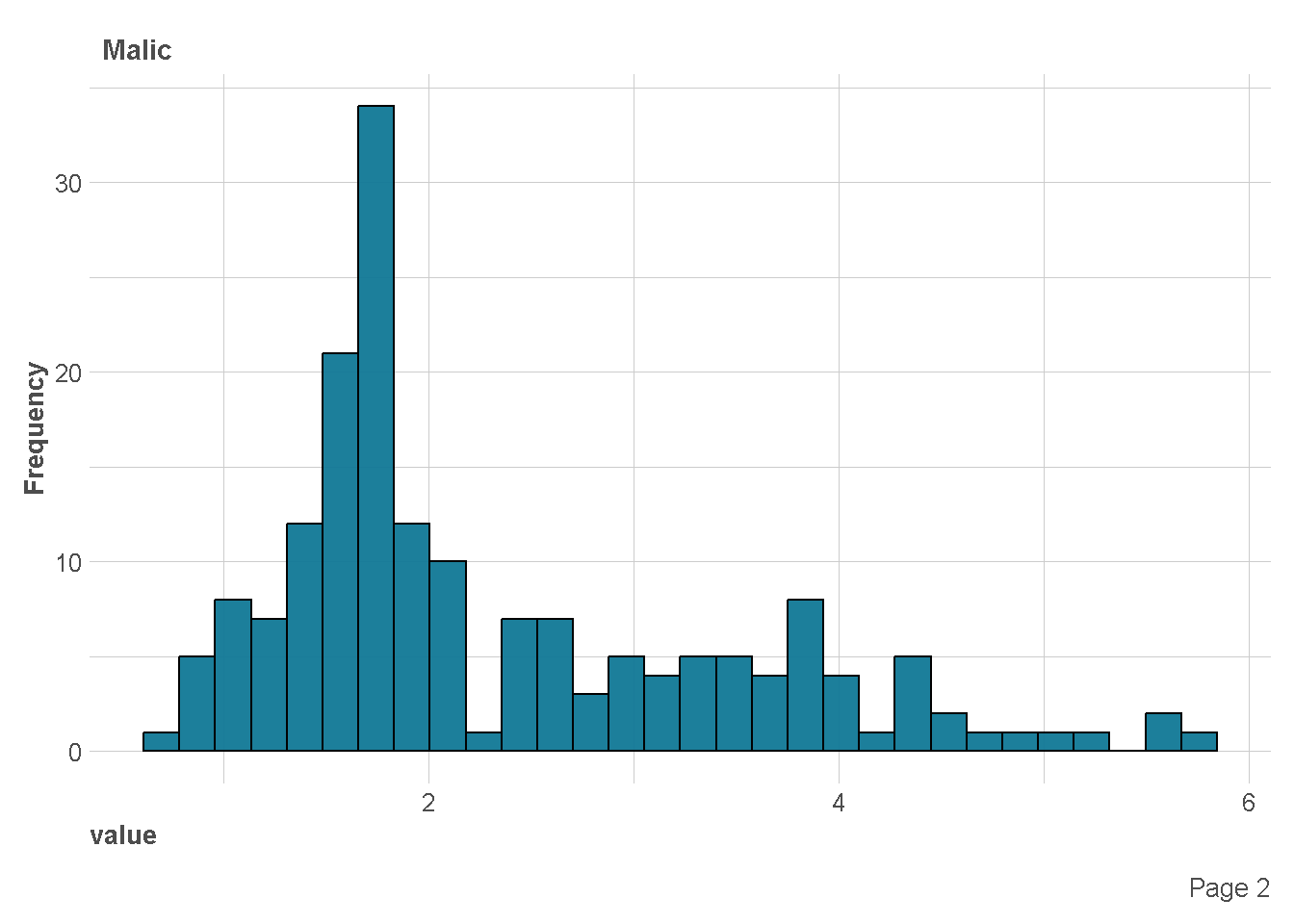
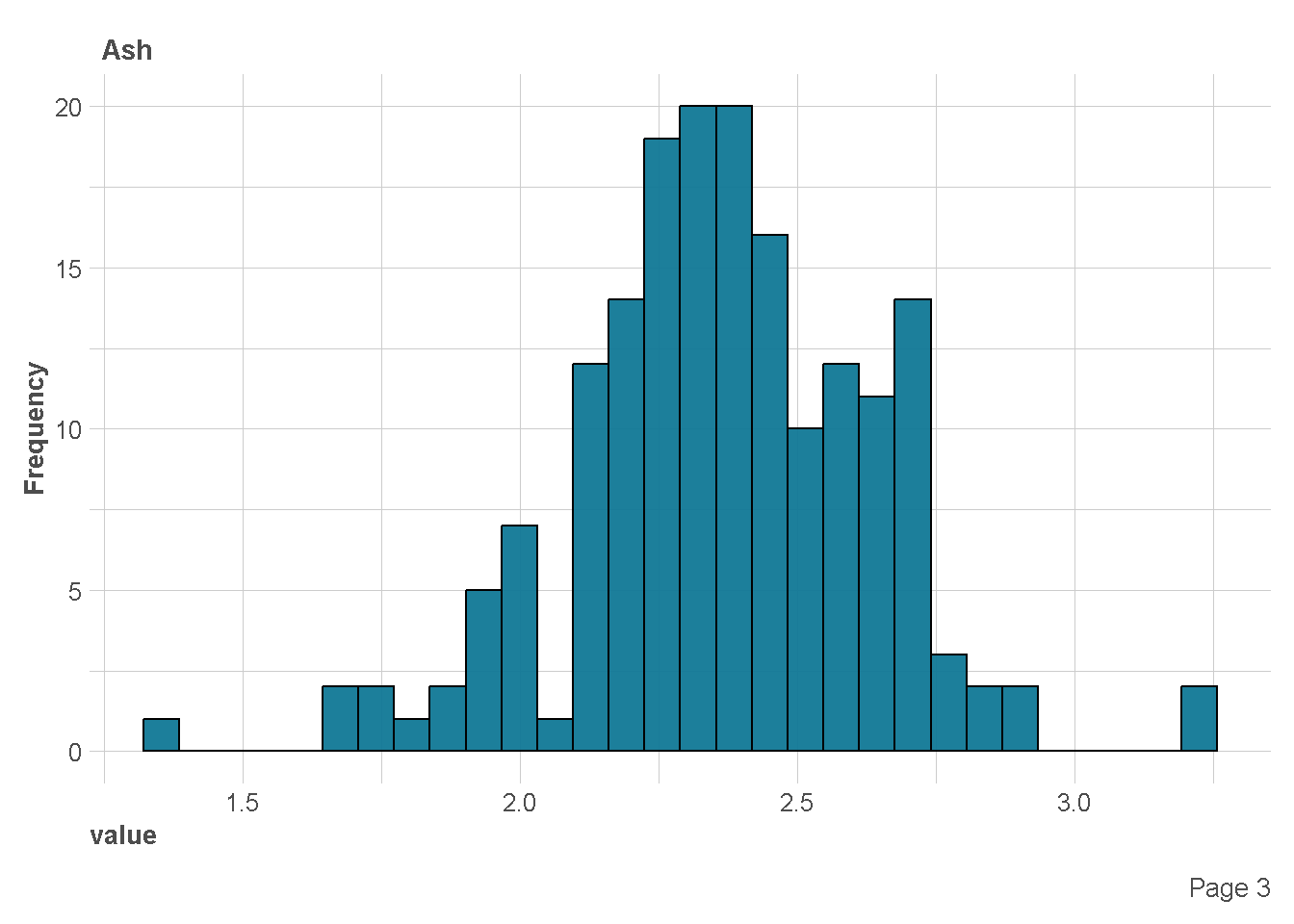
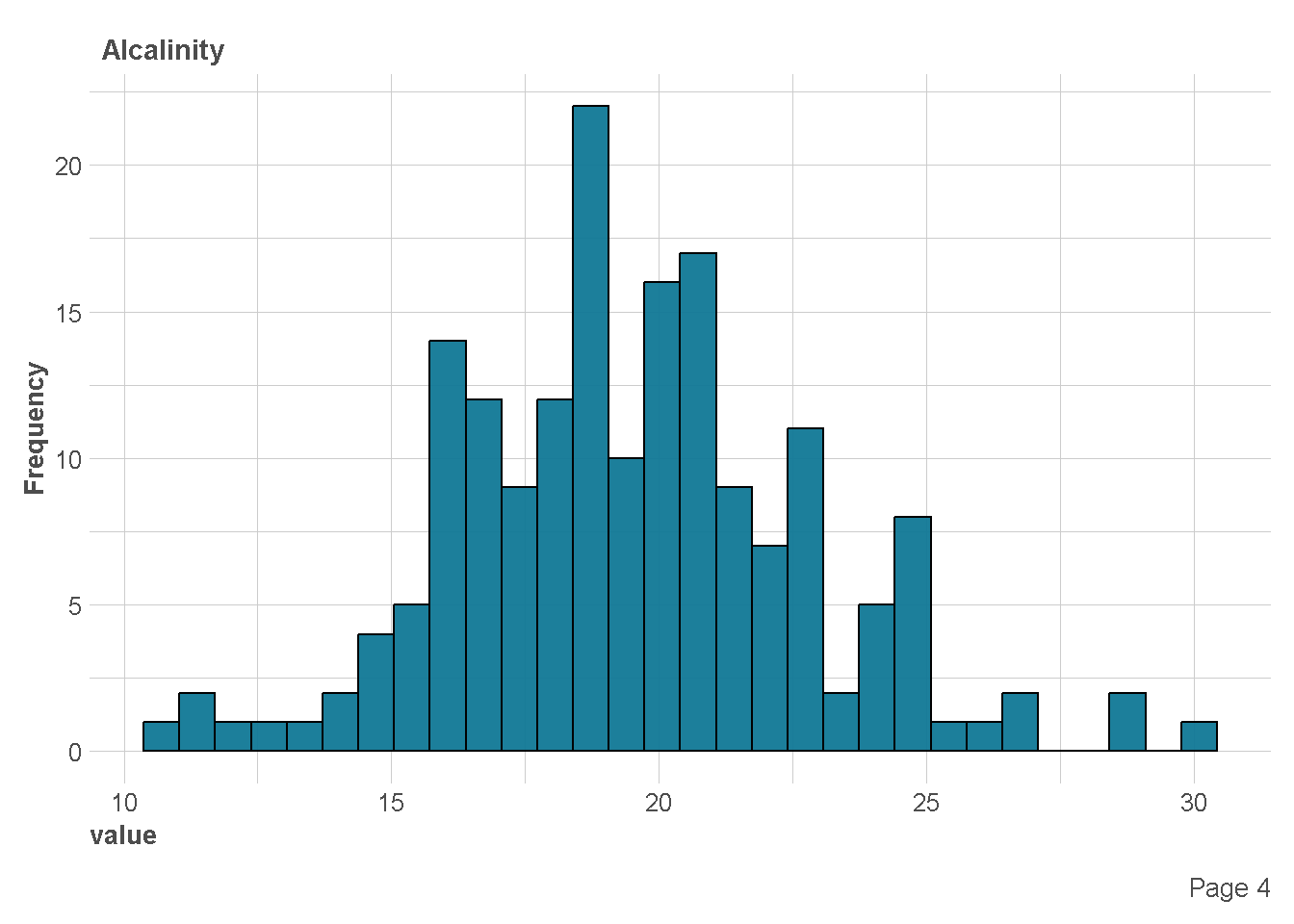
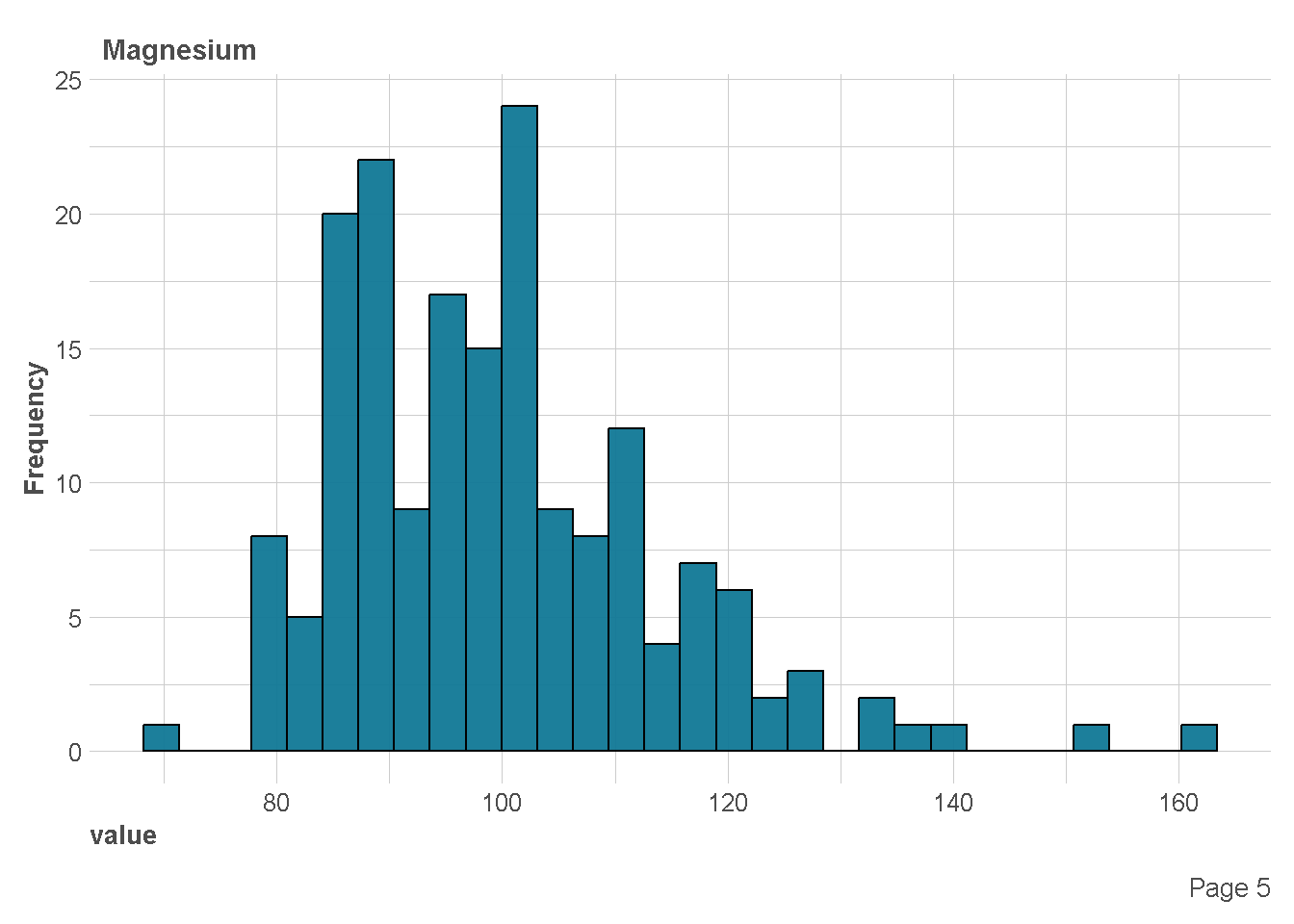
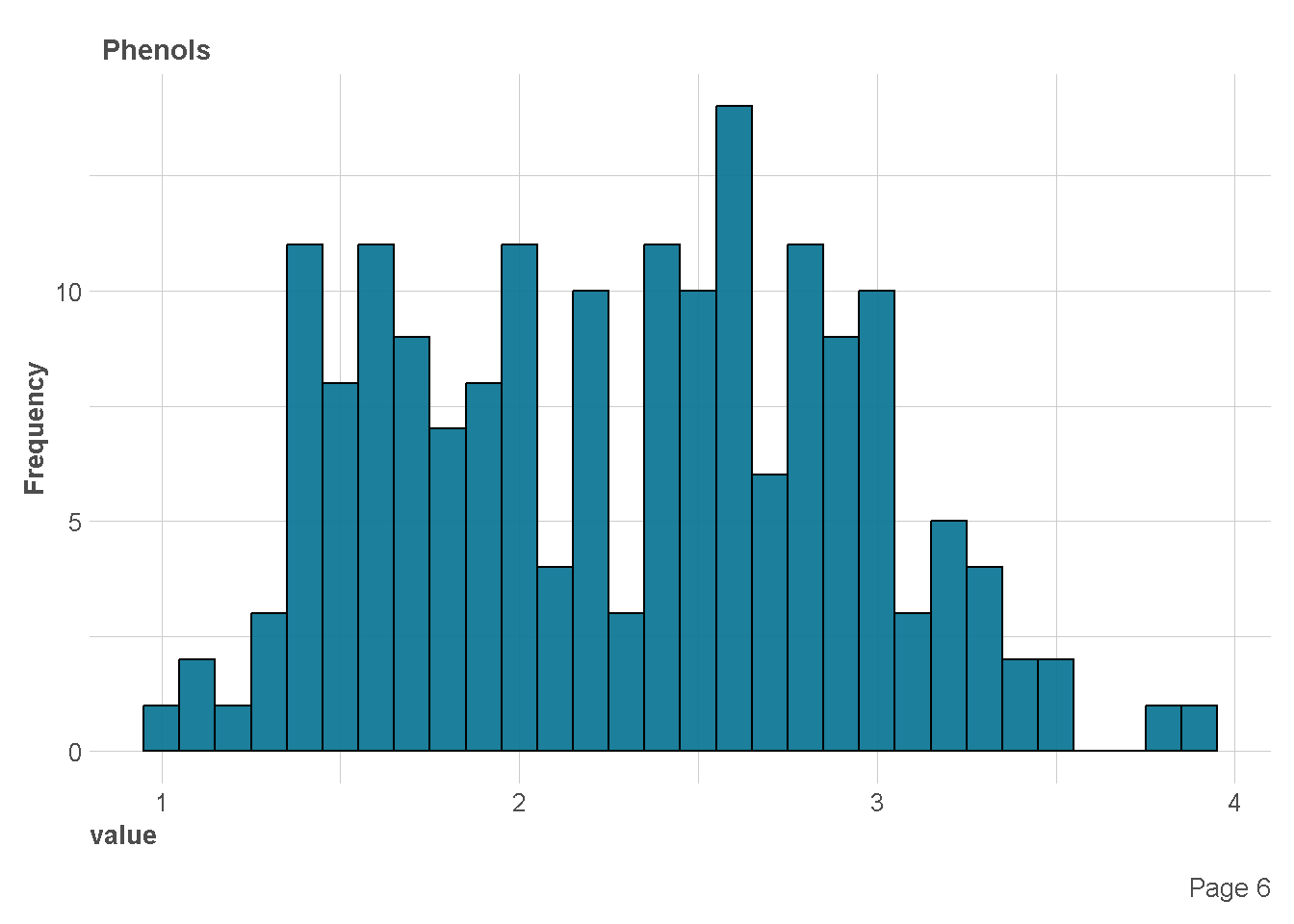
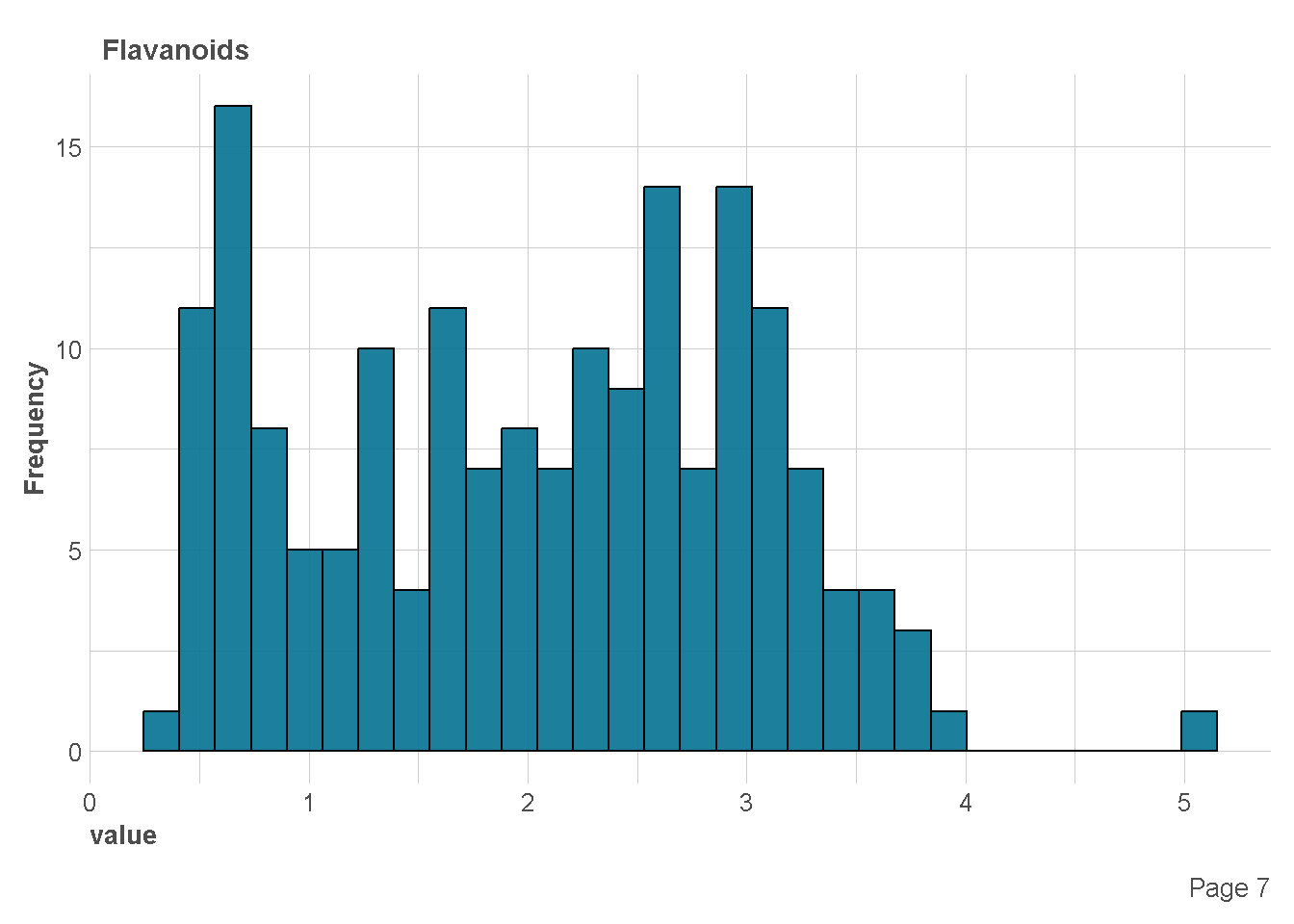
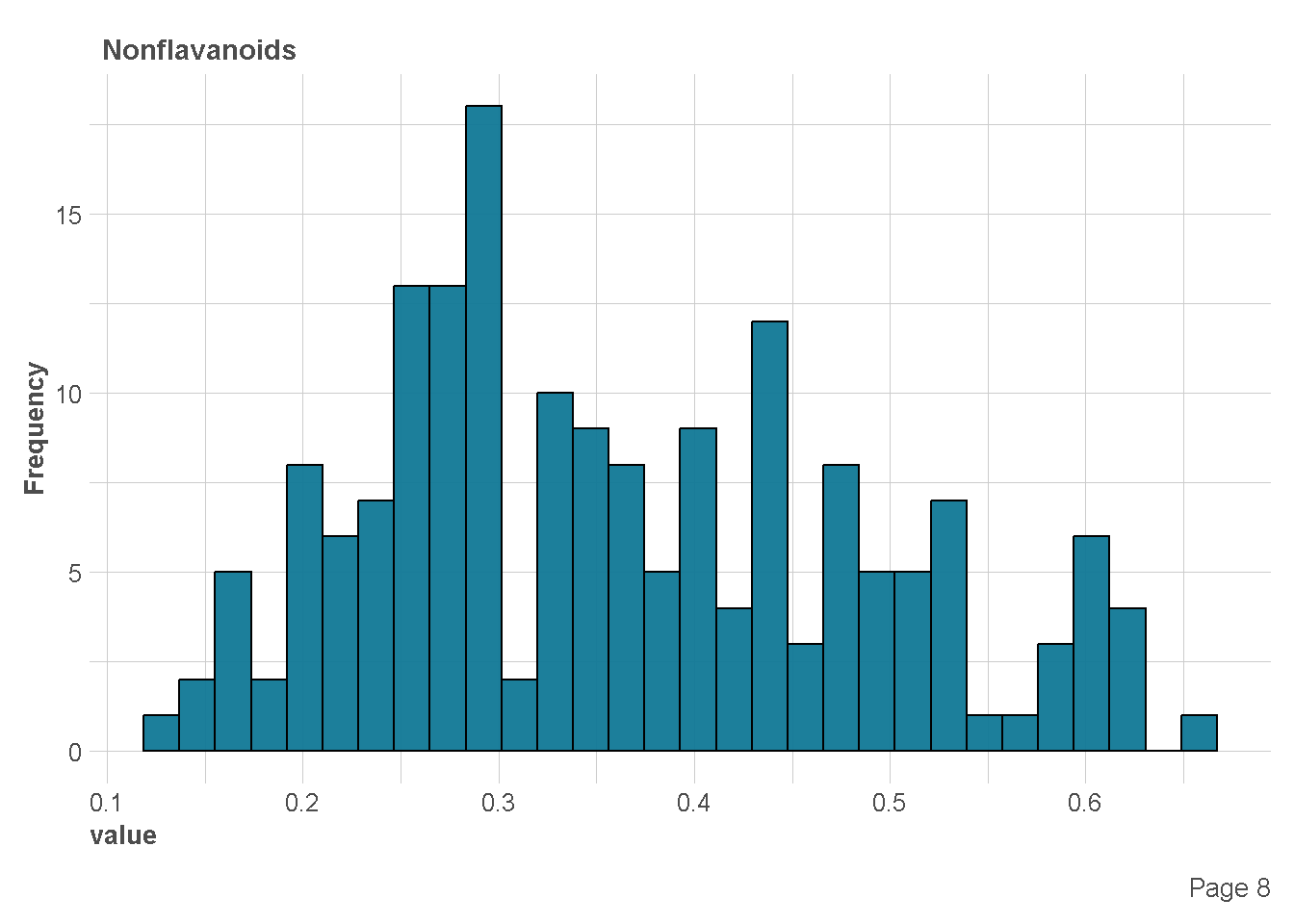
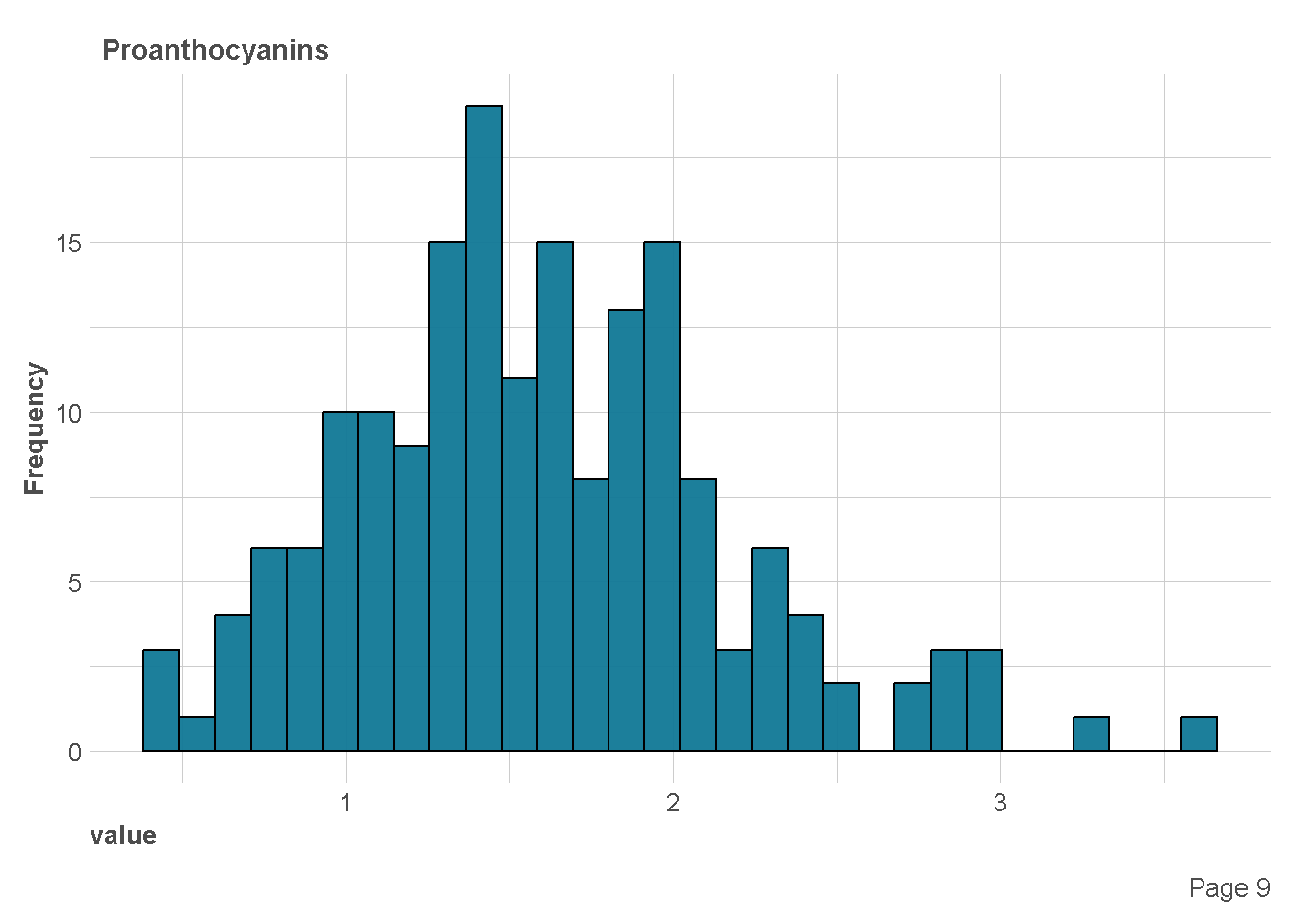
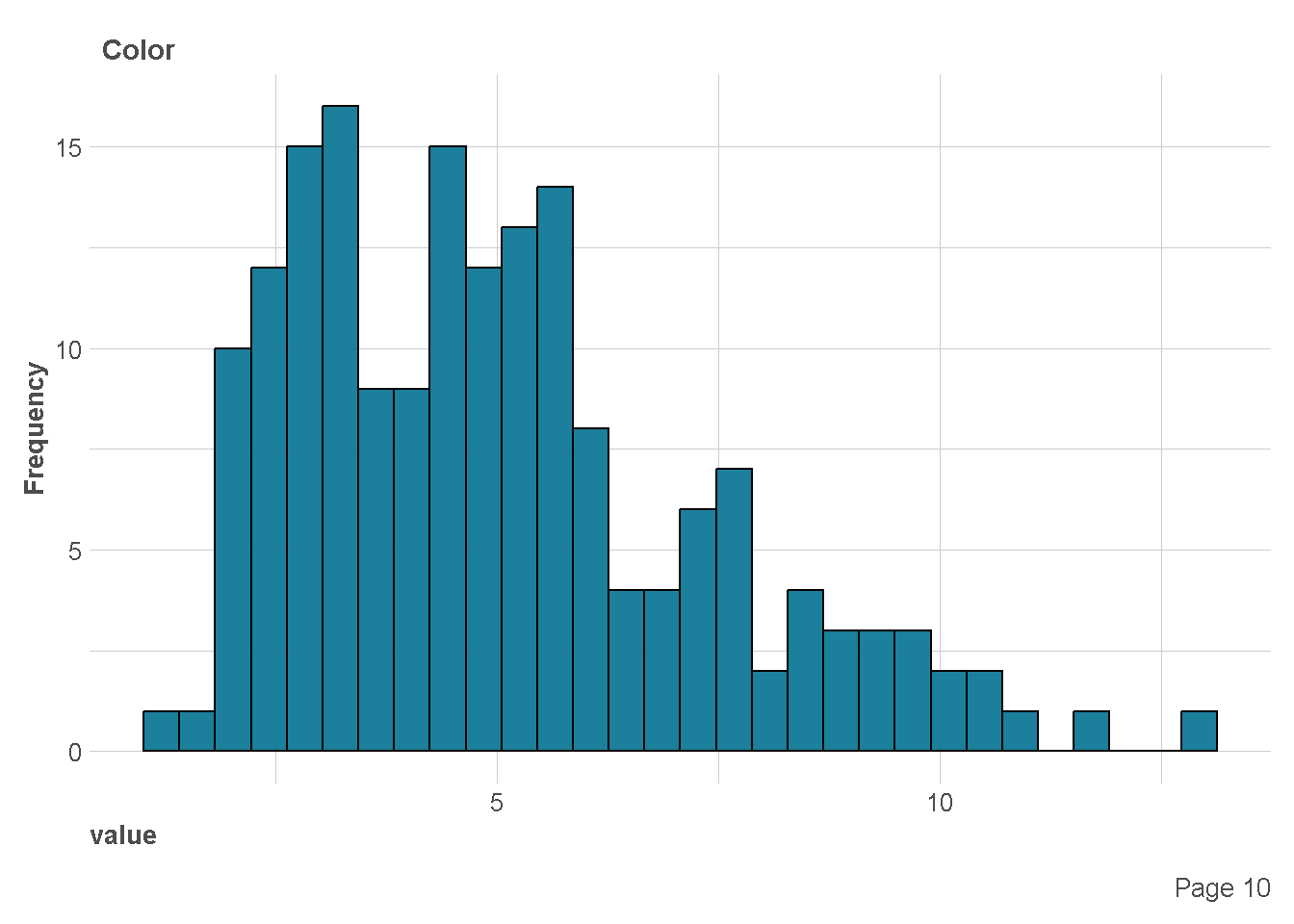
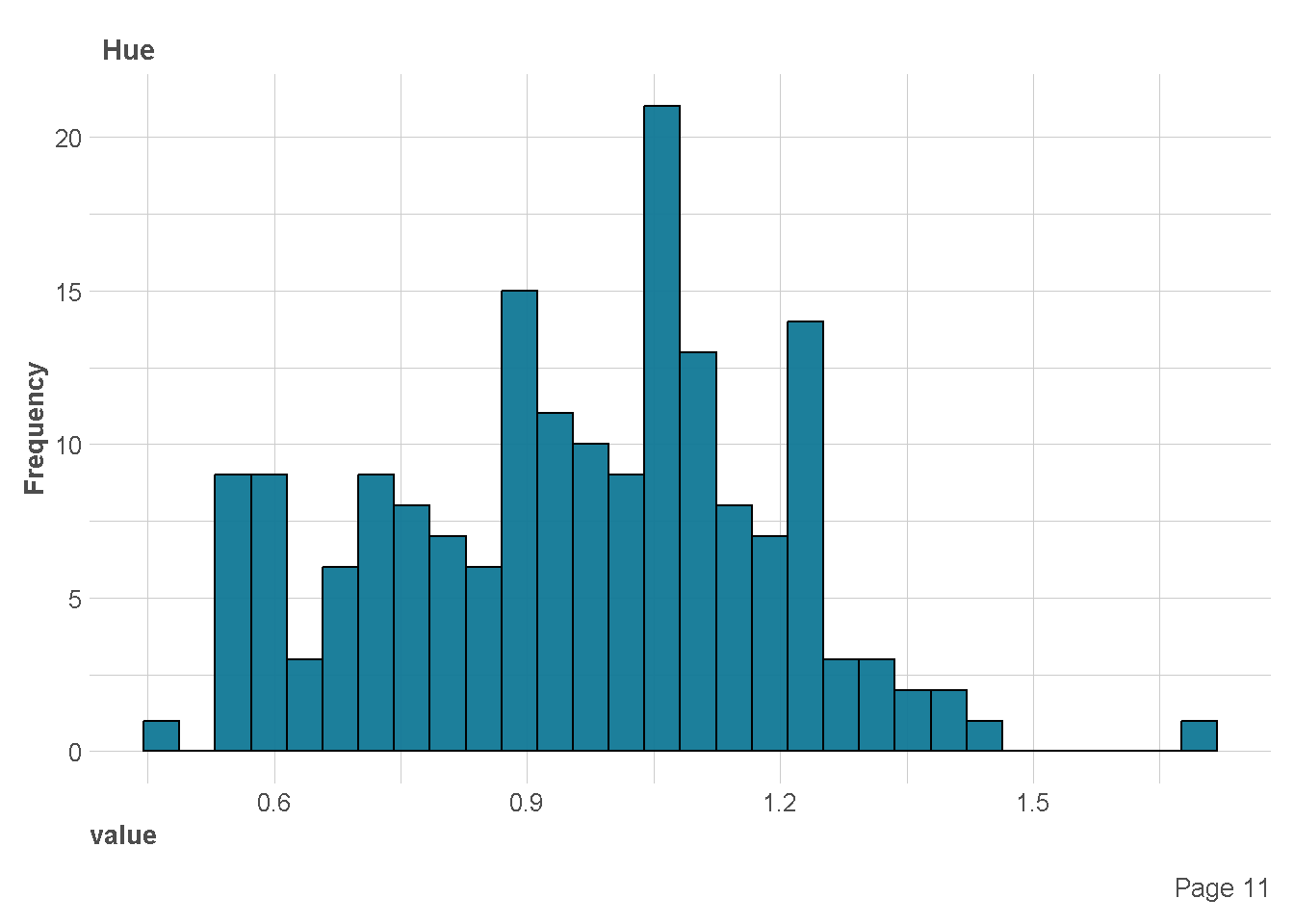
df %>% 
  select(where(is.numeric)) %>% 
  pivot_longer(cols = everything(),
               names_to = "variables",values_to = "value") %>% 
    plot_boxplot(by = "variables",
             geom_boxplot_args = list(fill="steelblue",
             col="black"),
             ggtheme = theme_minimal())

Ekplorasi Kategorik vs Numerik

df %>% 
  ExpNumViz(target = "Type",
            type = 2)
[[1]]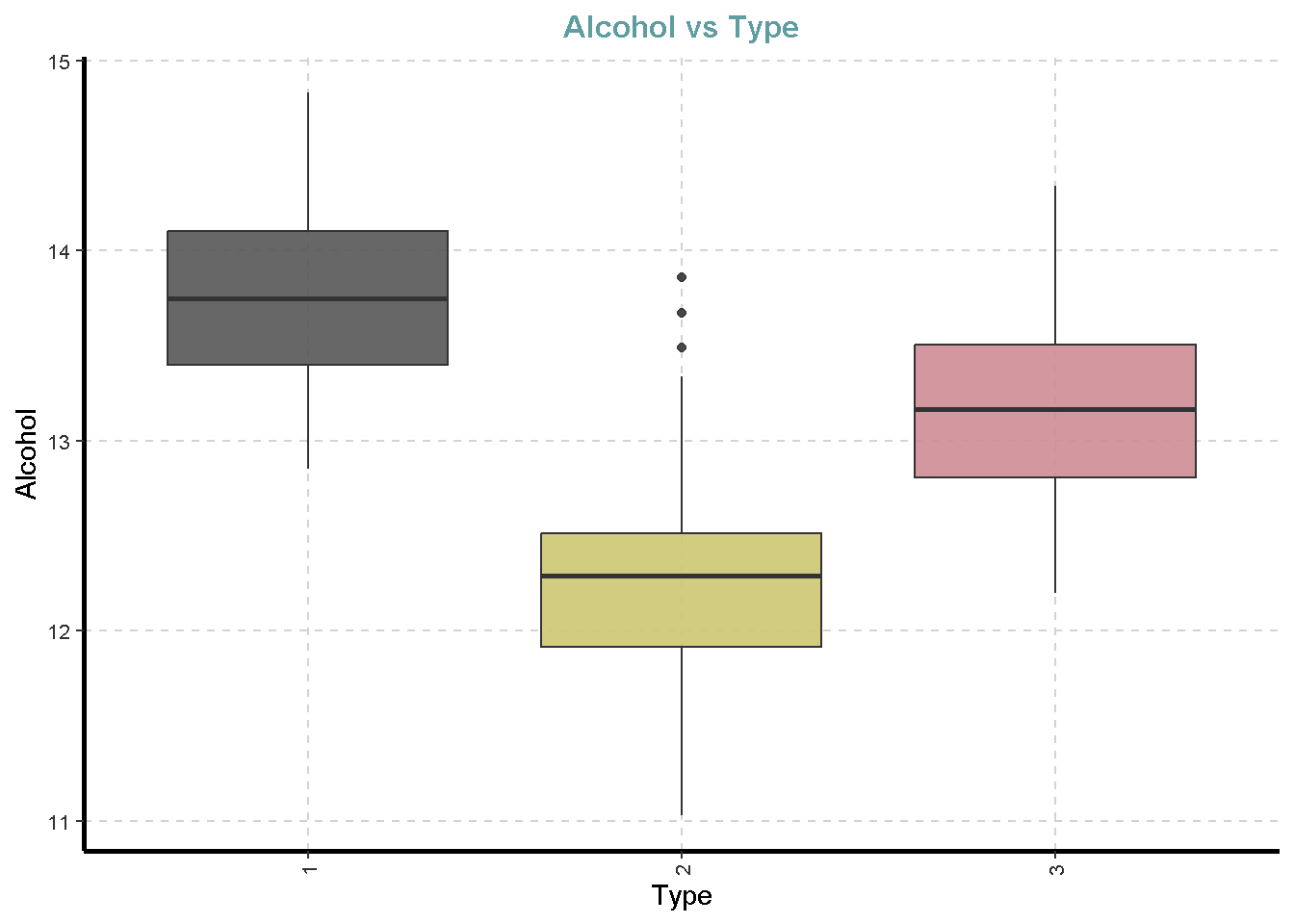


[[2]]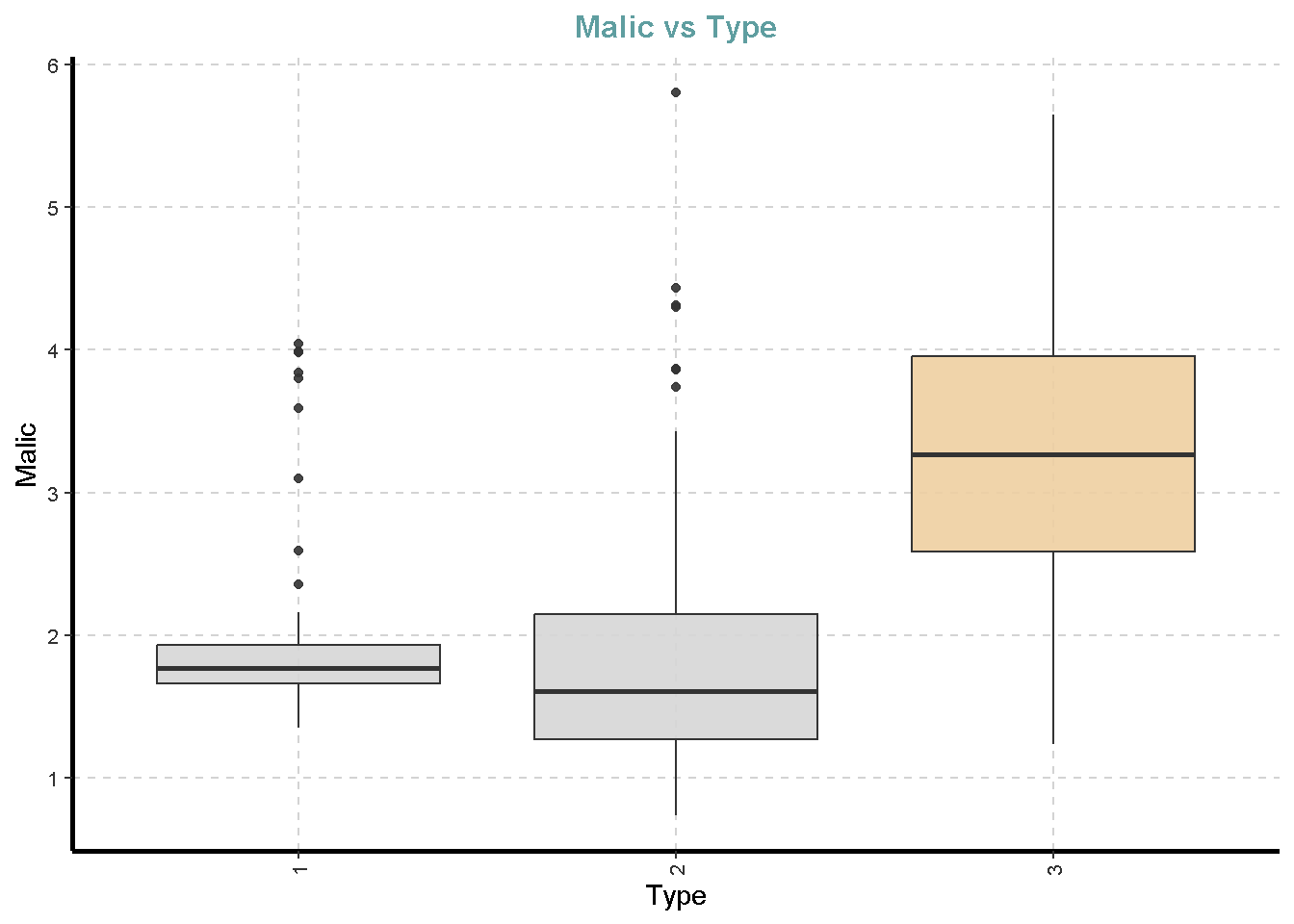


[[3]]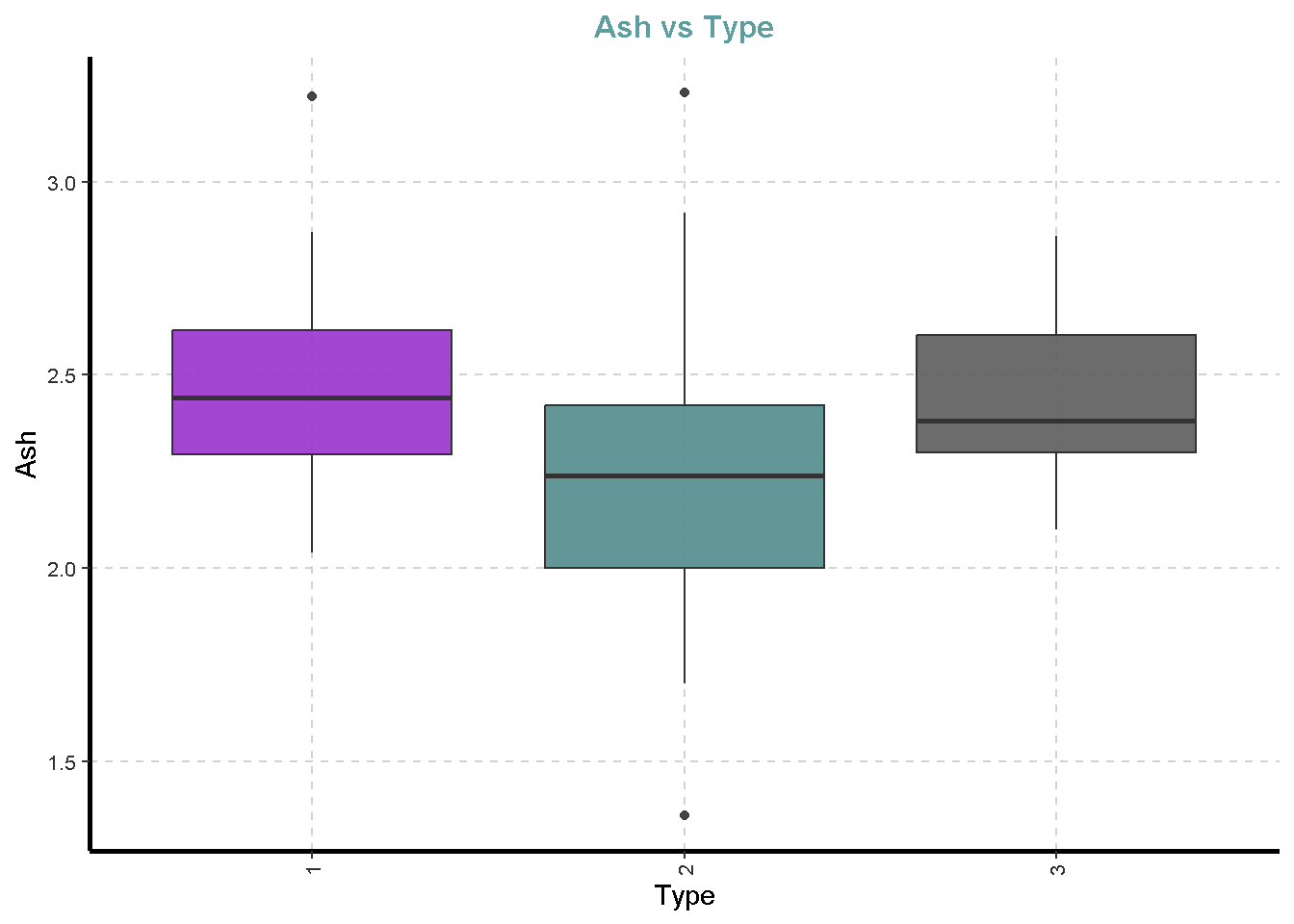


[[4]]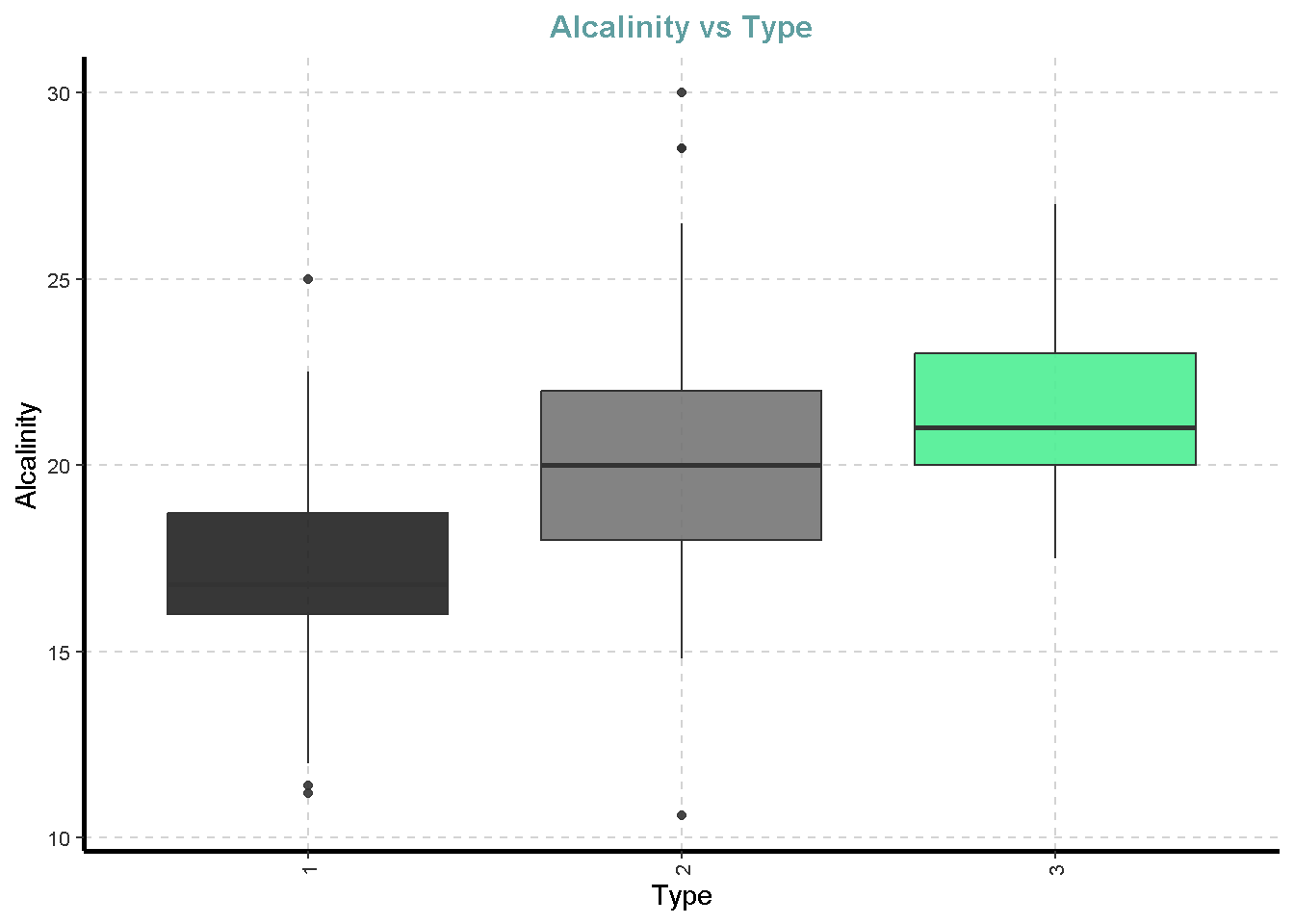


[[5]]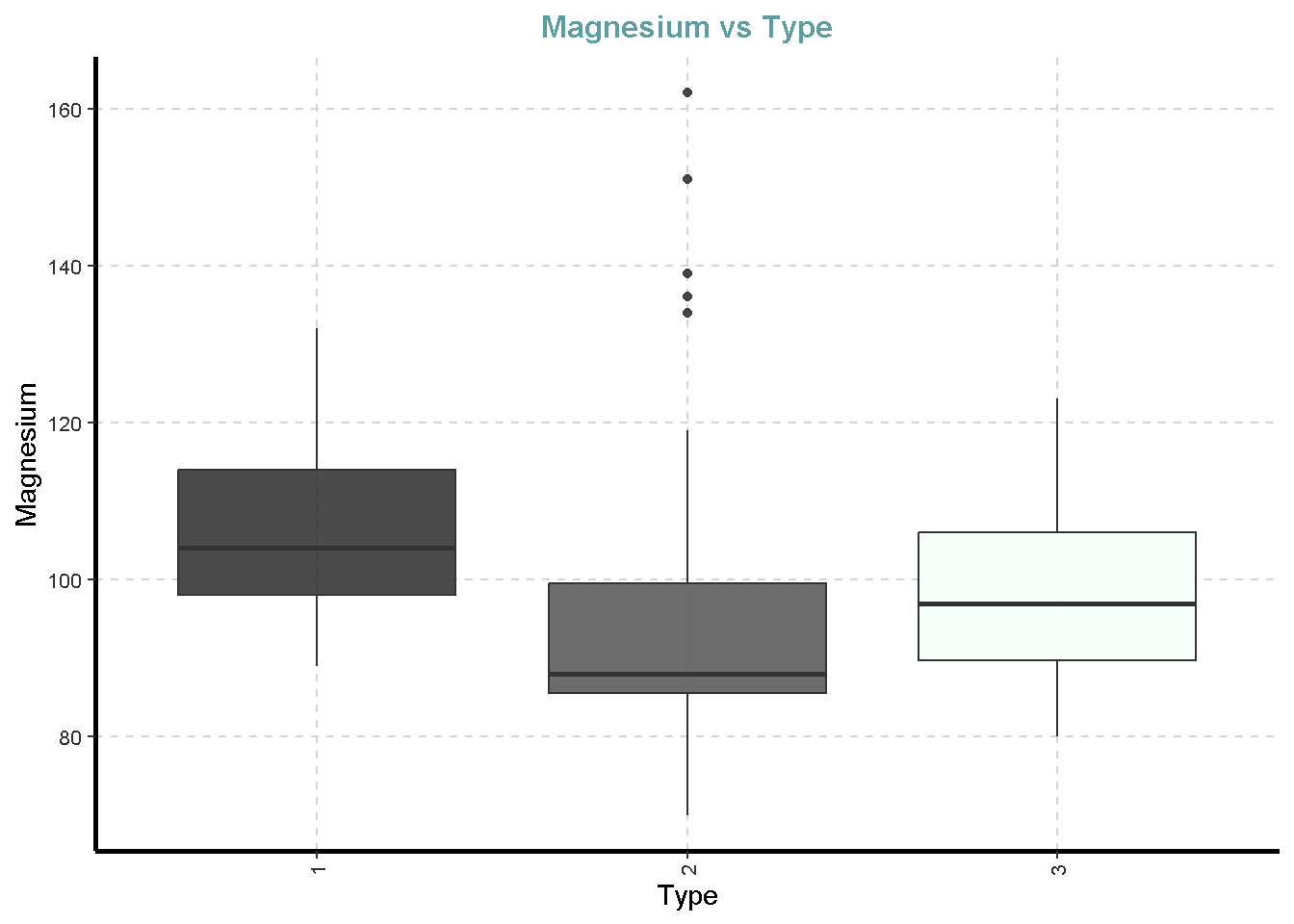


[[6]]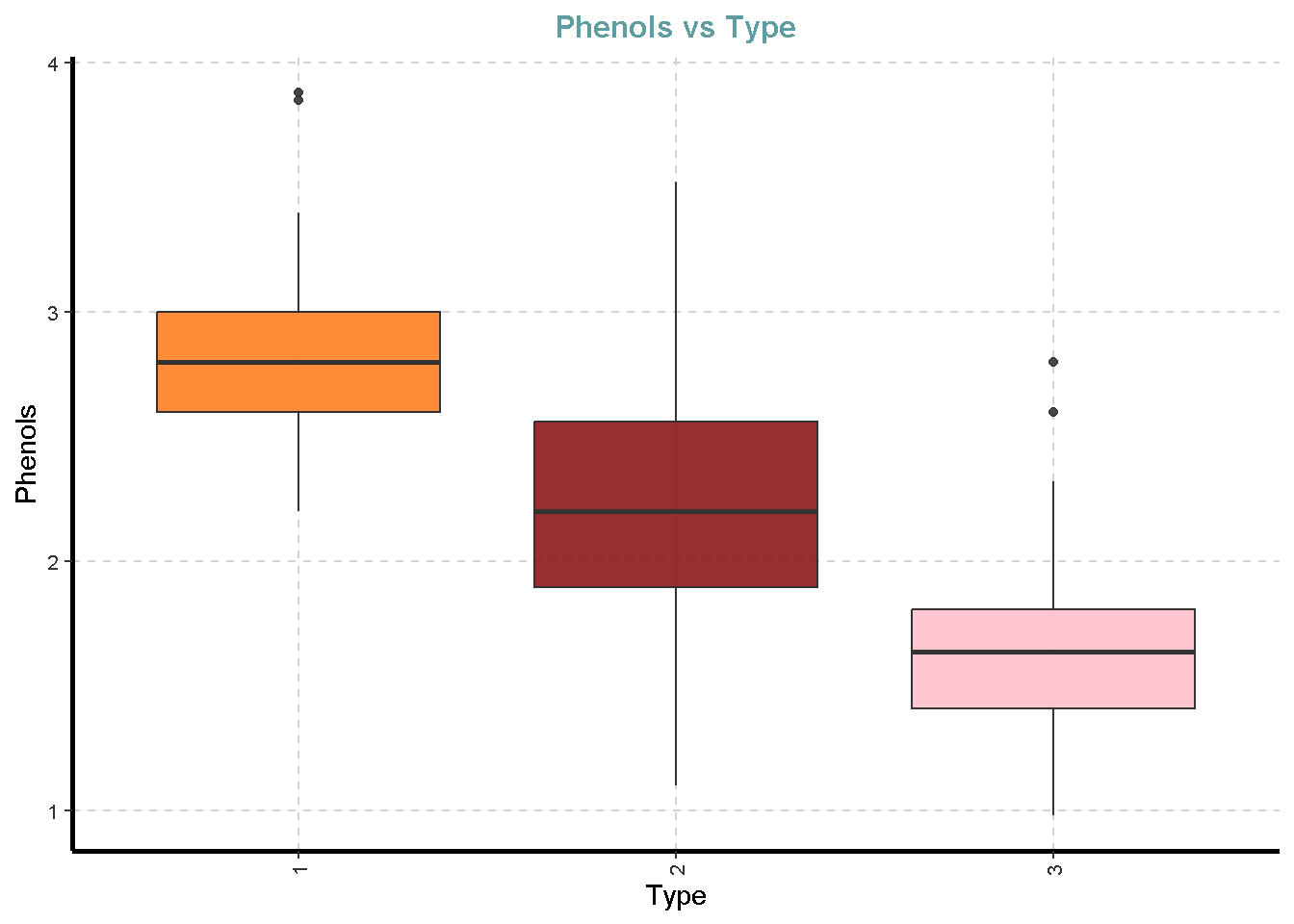


[[7]]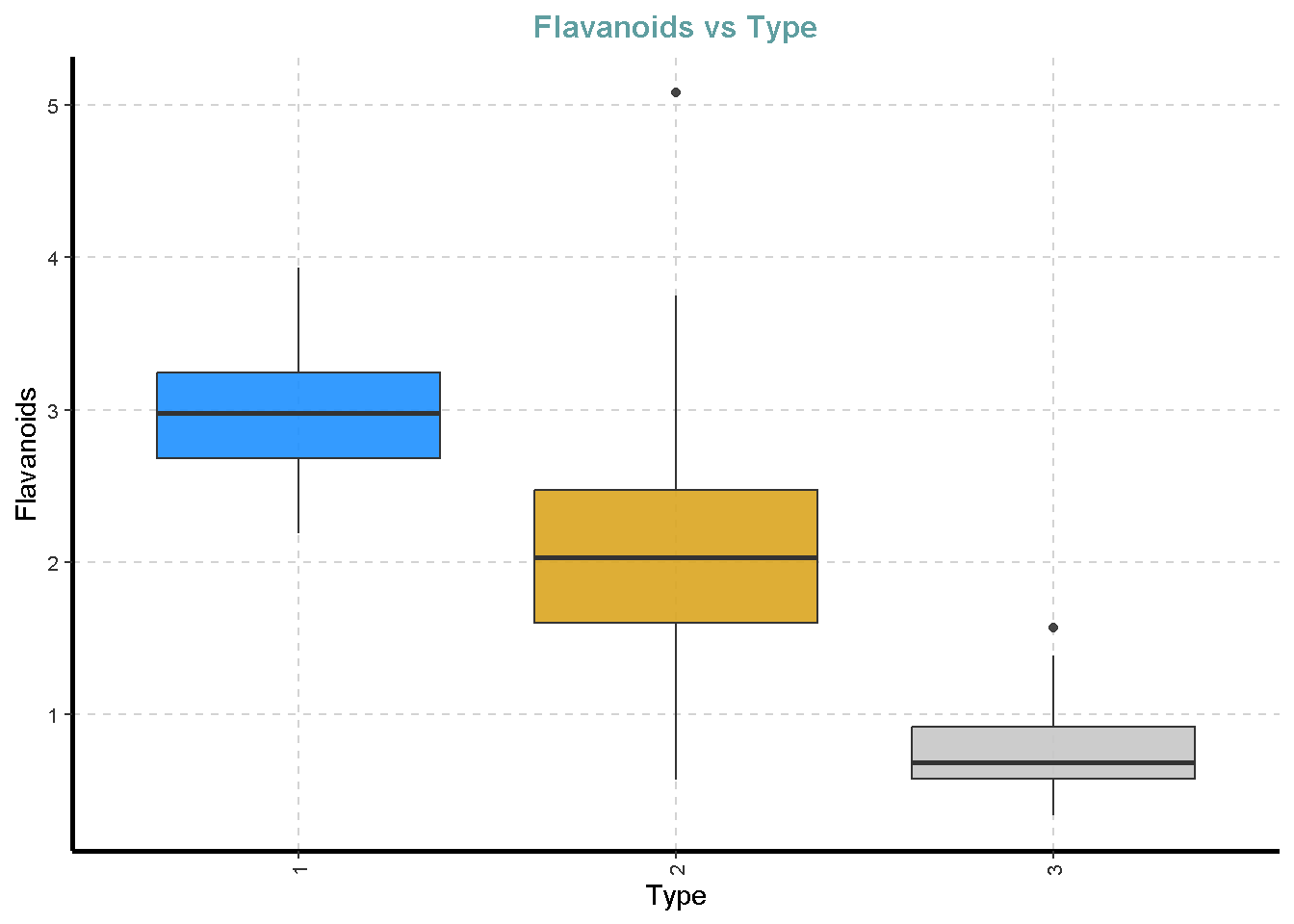


[[8]]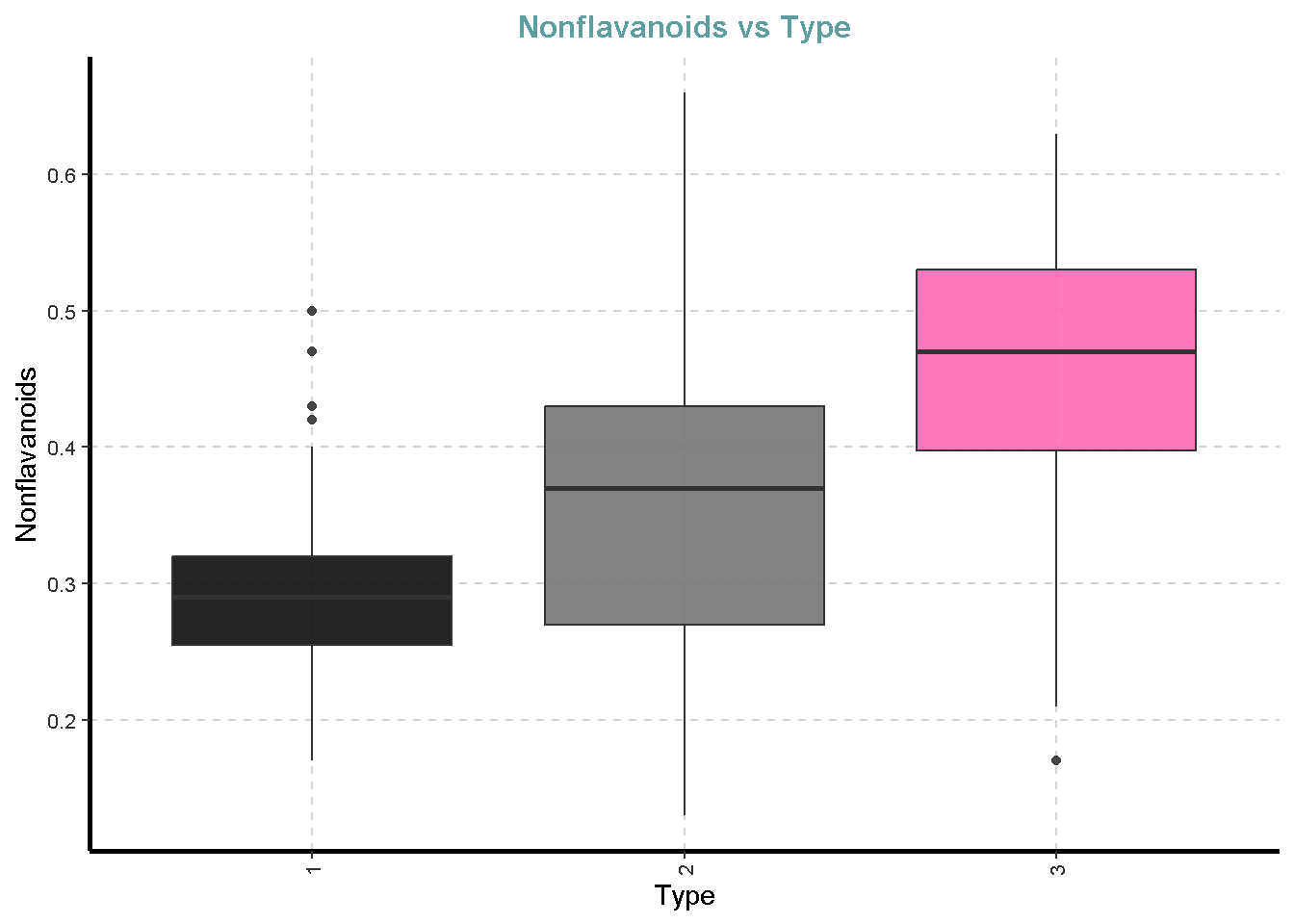


[[9]]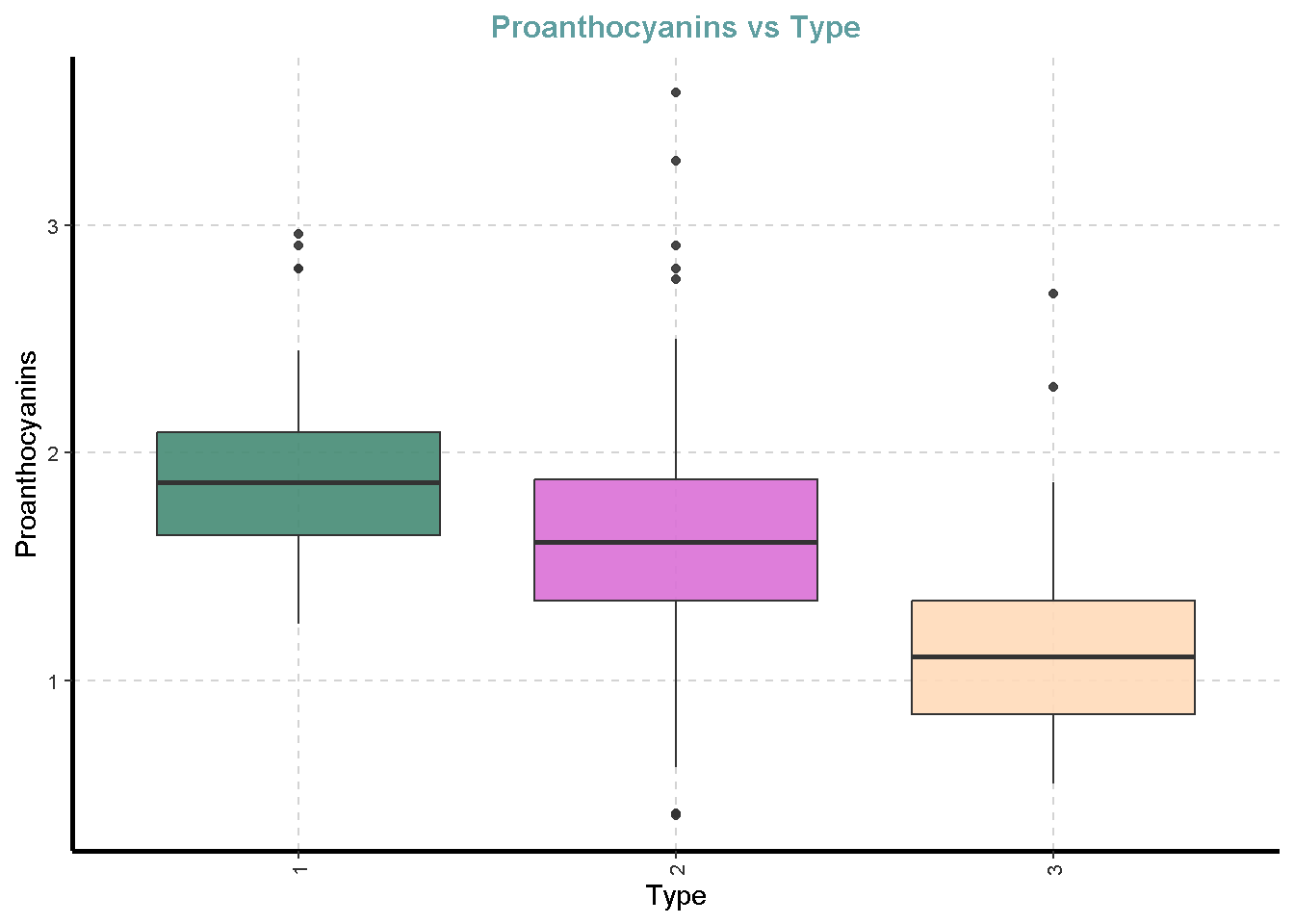


[[10]]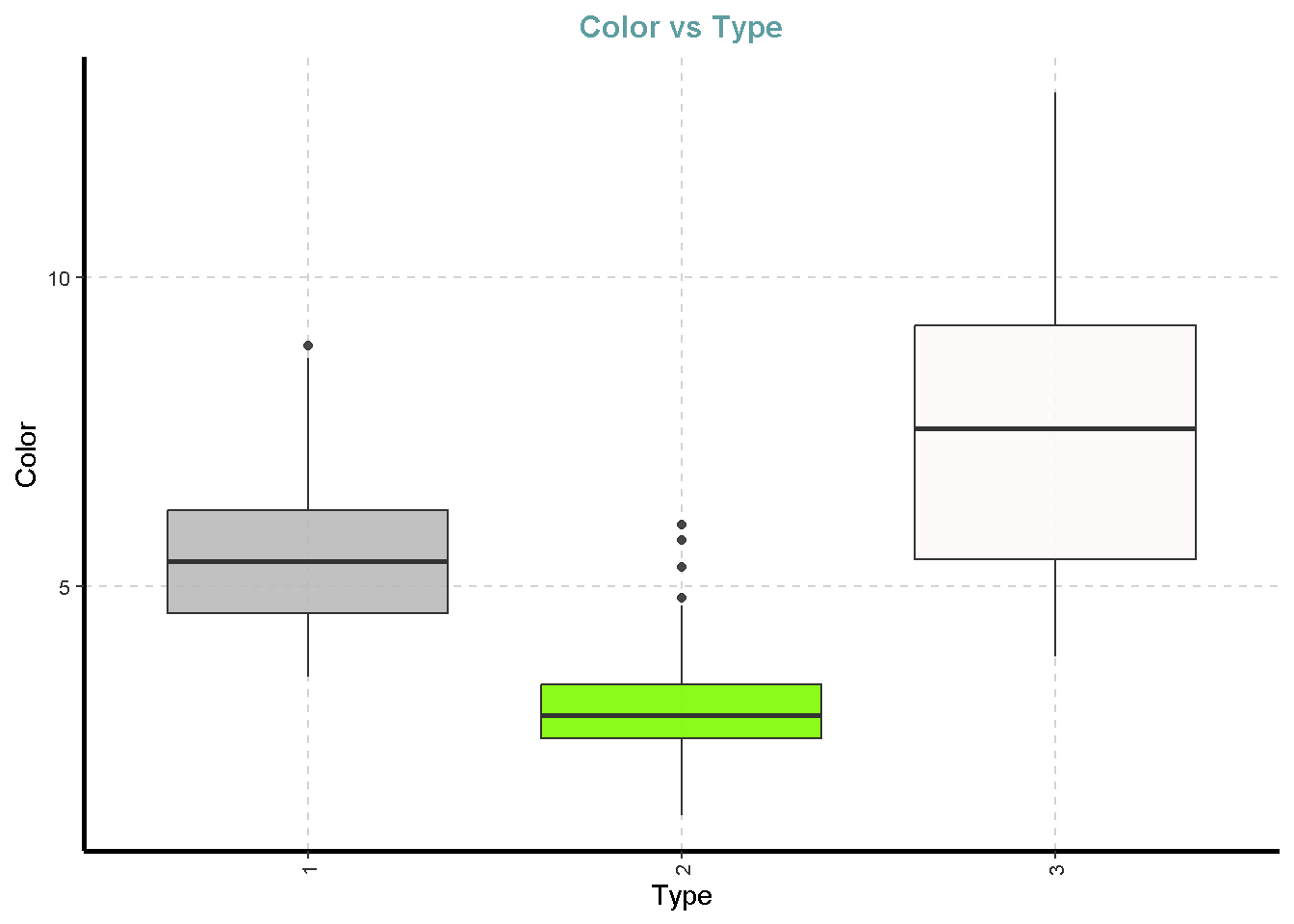


[[11]]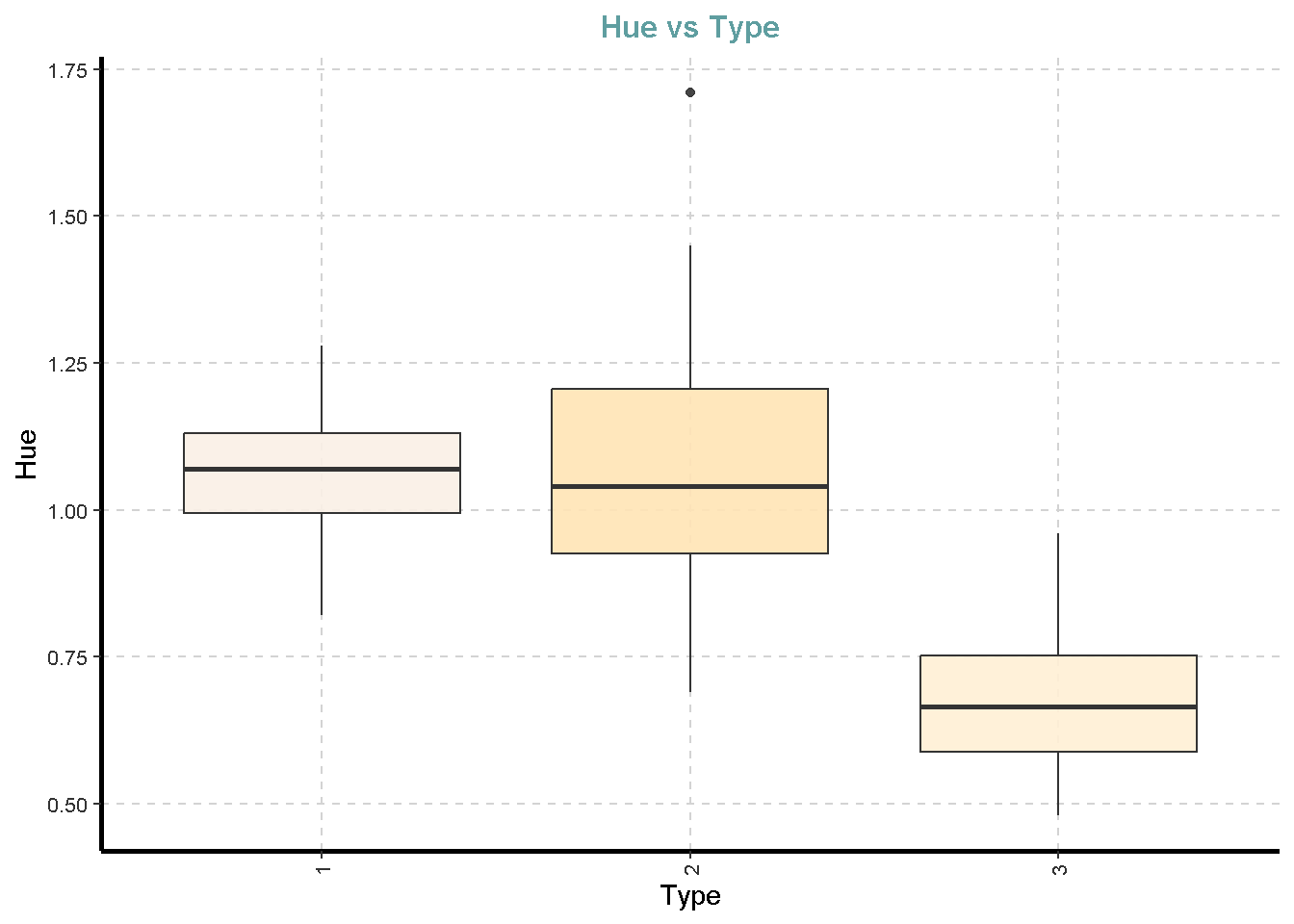


[[12]]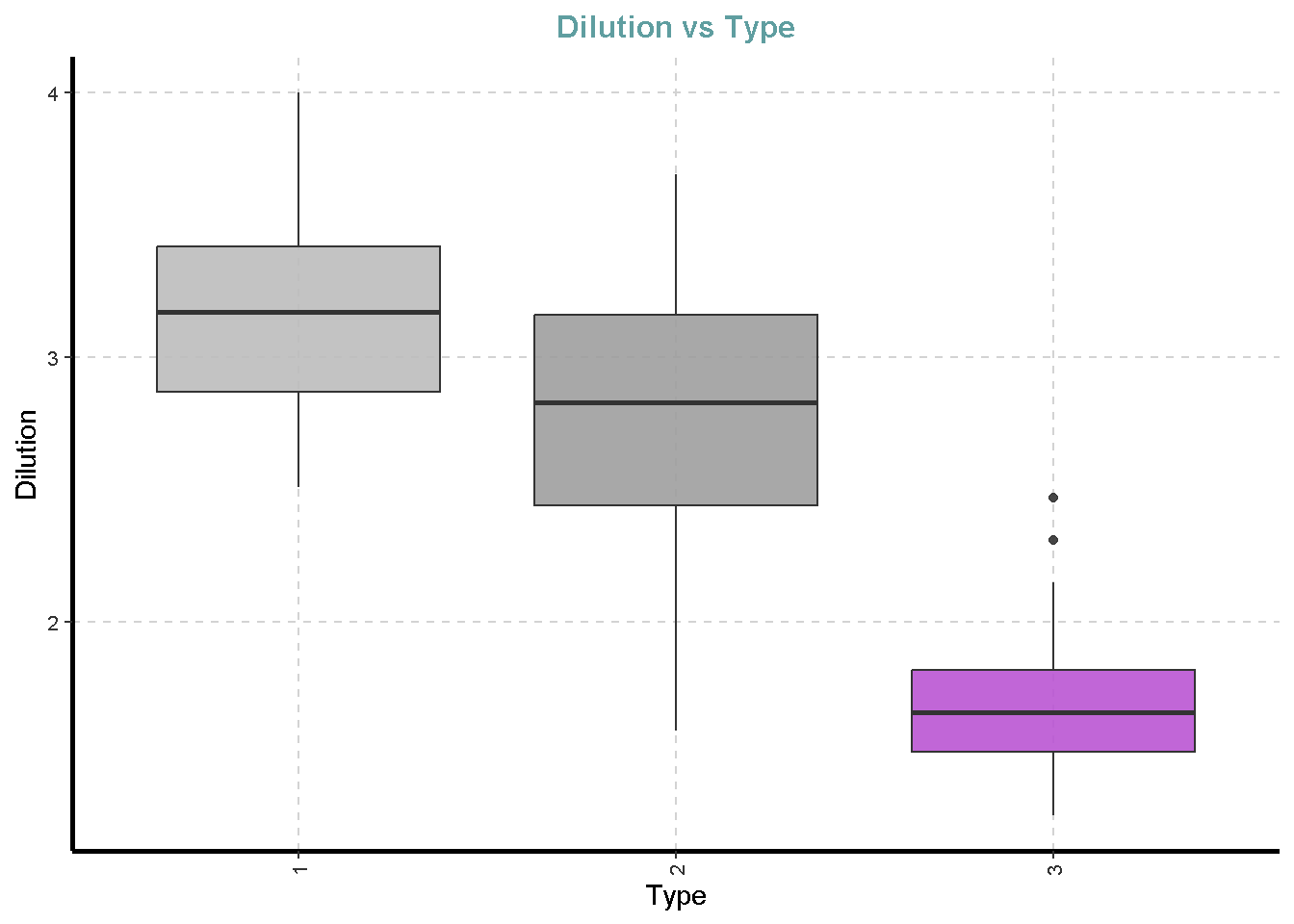


[[13]]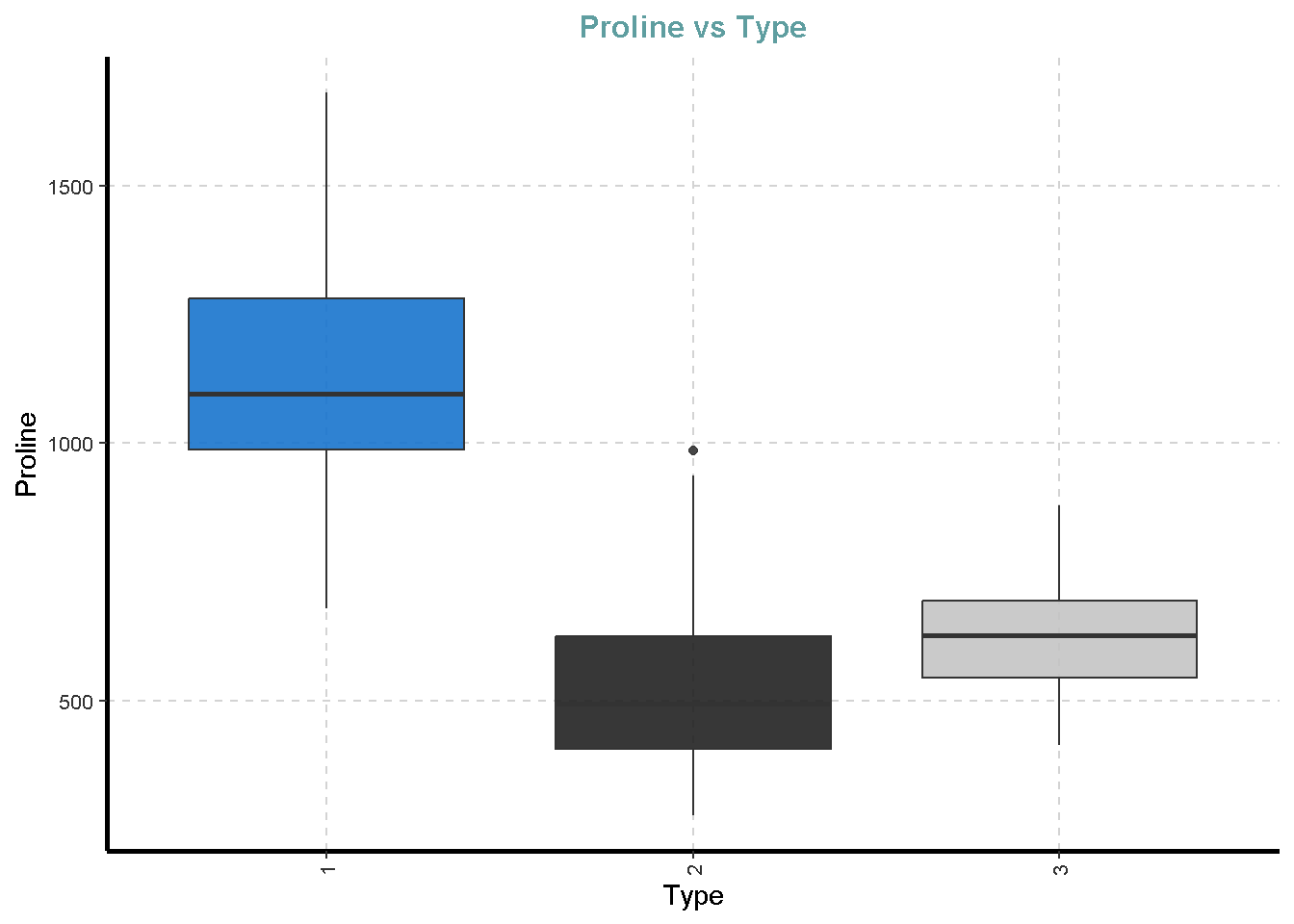

Deteksi Missing Value

df %>% 
  plot_missing(missing_only = FALSE,
             ggtheme = theme_lares())
Warning: `aes_string()` was deprecated in ggplot2 3.0.0.
ℹ Please use tidy evaluation idioms with `aes()`.
ℹ See also `vignette("ggplot2-in-packages")` for more information.
ℹ The deprecated feature was likely used in the DataExplorer package.
  Please report the issue at
  <https://github.com/boxuancui/DataExplorer/issues>.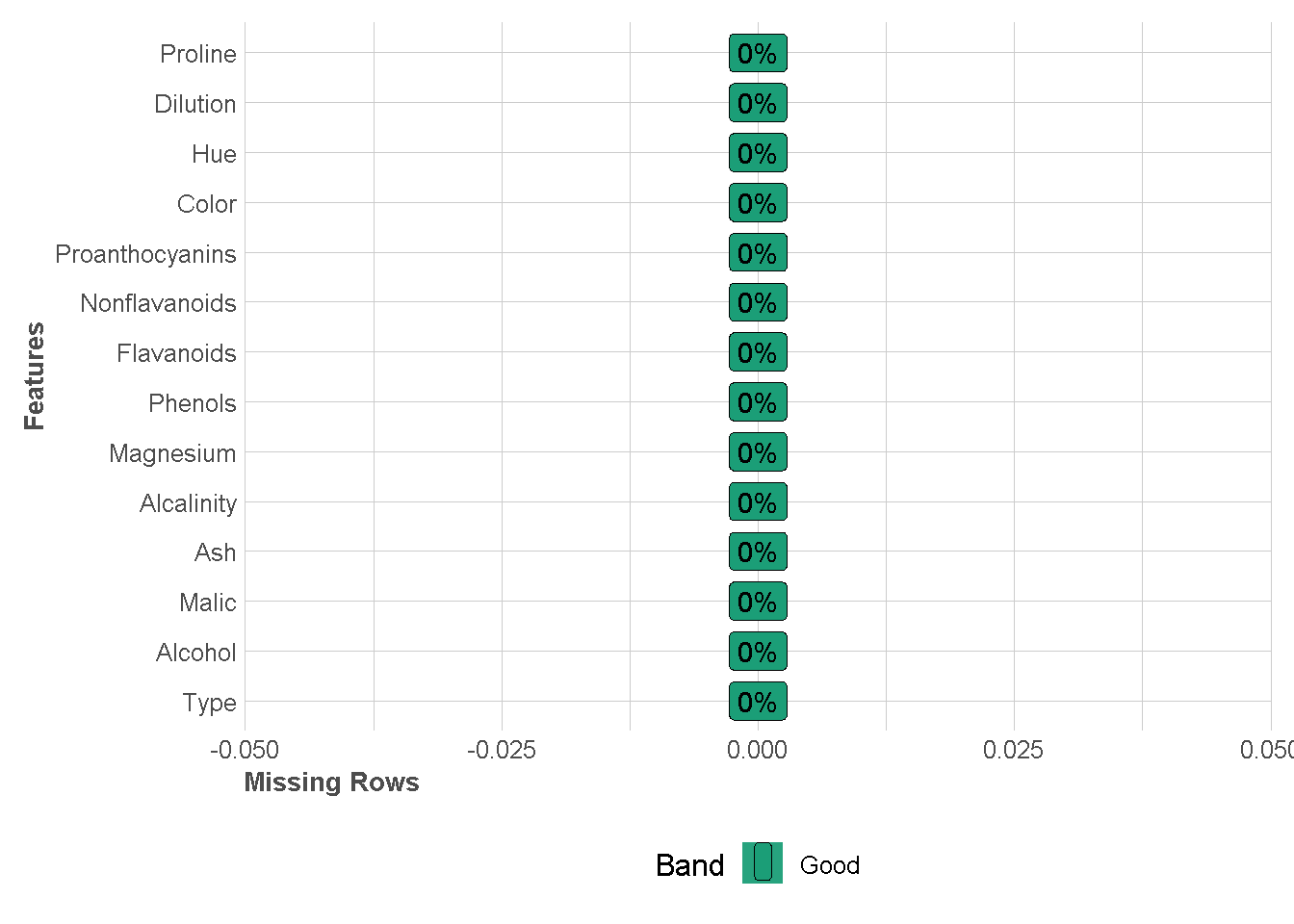

Analisis Diskirminant

Fungsi diskriminan dari Linear Discriminant Analysis (LDA) dapat dituliskan sebagai berikut:

\[ \boldsymbol{d}(\boldsymbol{x})=\log{P(\boldsymbol{y}=k|\boldsymbol{x})}=b_{0}+b_{1}\boldsymbol{x}_{1}+b_{2}\boldsymbol{x}_{2}+\ldots+b_{p}\boldsymbol{x}_{p} \]

dengan:

  • \(\boldsymbol{y}\) adalah variabel respon dengan \(k\) kelas (kategori)
  • \(\boldsymbol{d}(\boldsymbol{x})\) adalah skor diskriminan
  • \(b_{0},b_{1},b_{2},\dots,b_{p}\) adalah koefisien atau bobot diskriminan
  • \(\boldsymbol{x}_{1},\boldsymbol{x}_{2},\ldots,\boldsymbol{x}_{p}\) adalah variabel prediktor

Asumsi dari LDA antara lain adalah:

  1. Setiap amatan harus dikelompokkan hanya ke dalam satu kelas (kategori) saja
  2. Ragam dalam setiap kelas (kategori) adalah sama (equal variances)
  3. \(\boldsymbol{x}_{1},\boldsymbol{x}_{2},\ldots,\boldsymbol{x}_{p}\) berdistribusi normal ganda (multivariate normal distribution)

LDA dapat dilakukan bila terdapat perbedaan yang nyata antar kelas (kategori), sehingga pada tahap awal yang harus dilakukan adalah uji hipotesis bahwa tidak ada perbedaan kelas (kategori) di antara amatan.

Jika asumsi Ragam dalam setiap kelas (kategori) adalah sama tidak terpenuhi maka maka gunakan Quadratic Discriminant Analysis (QDA).

Note : Menurut Mattjik dan Sumertajaya pada buku Sidik Peubah Ganda, “umumnya sangat sulit sekali untuk dapat memenuhi persyaratan 2 dan 3, yang dalam praktek sering kali tidak diuji; hal mana akan membuat akurasi dari analisis dengan fungsi diskriminan akan berkurang. Namun demikian, fungsi diskriminan selalu menghasilkan estimasi yang kokoh (robust estimates) terutama yang berkaitan dengan prediksi kelas”.

Pemeriksaan Awal

Pada tahap ini kita akan memeriksa asumsi 2 dan 3 LDA serta memeriksa apakah ada perbedaan kelas (kategori) di antara amatan.

Uji Normal Ganda (Multivariate Normal) setiap kelas variabel respon

Hipotesis yang diuji adalah sebagai berikut

\[ \begin{aligned} H_0 &: \text{data menyebar normal ganda} \\ H_1 &: \text{data tidak menyebar normal ganda} \end{aligned} \]

Untuk menguji kenormalan ganda di R, bisa menggunakan fungsi mvn dari package MVN. fungsi mvn memiliki beberapa uji normal ganda yang bisa dilakukan. Pemilihan uji normal ganda bisa dilakukan melauli argumen mvnTest, seperti uji Mardia (mvnTest="mardia"), uji Henze-Zirkler(mvnTest="hz"), uji Royston (mvnTest="royston"),uji Doornik-Hansen (mvnTest="dh") dan uji energy mvnTest="energy". Argumen subset diisi dengan kolom data yang dijadikan sebagai variabel respon.

uji_normalGanda <- MVN::mvn(data = df,subset="Type",mvn_test = "hz")
uji_normalGanda$multivariate_normality

Karena nilai dari p-value dari $1 dan $3 adalah 0.198733 dan 0.3721148, yang mana lebih besar dari nilai \(\alpha= 0.05\) maka dapat disimpulkan bahwa tidak cukup bukti untuk menolak \(H_0\). Artinya untuk peubah-puebah prediktor pada wine tipe 1 dan tipe 3 berdistribusi normal ganda. Sementera itu, p-value dari $2 sangat kecil yaitu 4.160195e-06 yang mana lebih kecil dari nilai \(\alpha=0.05\). Artinya peubah-puebah penjelas pada wine tipe 2 tidak berdistribusi normal ganda.

Walaupun ada satu kelas yang tidak memenuhi asumsi normal ganda kita akan tetap lanjutkan menggunakan analisis diskriminan karena berdasarkan Matjik dan Sumertajaya fungsi diskriminan masih dapat menghasilkan kemampuan klasifikasi yang baik.

Uji Asumsi Kesamaan Ragam setiap kelas variabel respon

Hipotesis asumsi kesamaan ragam

\[ \begin{aligned} H_0 &: \text{ragam antar populasi sama} \\ H_1 &: \text{ragam antar populasi tidak sama} \end{aligned} \]

Uji kesamaan ragam bisa dilakukan dengan menggunkan fungsi boxM yang berasal dari package heplots. Fungsi ini hanya membutuhkan 2 argumen, yaitu data dalam bentuk data.frame atau matrix tanpa kolom gerombol (dalam hal ini kolom Type) dan vektor gerombol yang diperoleh dari data (dalam hal ini kolom Type).

Y_matrix <- df %>% 
  dplyr::select(-Type) %>% 
  as.matrix()
uji_ragam <- heplots::boxM(Y=Y_matrix,
                           group=df$Type)
parameters(uji_ragam) %>% 
  print_html()
Model Summary
Parameter1 Parameter2 z df p
Y_matrix df$Type 684.20 182 < .001

Karena nilai dari p-value dari uji Box’s M adalah kurang dari 2.891851e-59, yang mana lebih kecil dari nilai \(\alpha\) 0.05 maka dapat disimpulkan bahwa cukup bukti untuk menolak \(H_0\). Artinya ragam setiap kelas variabel respon tidak sama. Hal ini berarti model yang lebih cocok digunakan adalah QDA.

Warning

uji Box’s M sangat sensitif terhadap penyimpangan normalitas. Karena kelas Tipe 2 terbukti tidak berdistribusi normal ganda, hasil uji Box’s M bisa jadi “palsu” (menolak \(H_0\) karena ketidaknormalan, bukan karena perbedaan matriks kovarians)

alternatifnya kita bisa menggunakan Uji PERMDISP (Permutational Analysis of Multivariate Dispersions)

# 1. Buat matriks jarak Euclidean dari variabel numerik
dist_matrix <- vegan::vegdist(df %>% dplyr::select(-Type), method = "euclidean")
Registered S3 method overwritten by 'vegan':
  method          from   
  print.nullmodel parsnip
# 2. Jalankan uji PERMDISP
permdisp_model <- vegan::betadisper(dist_matrix, group = df$Type)
# 3. Uji signifikansinya (ANOVA pada jarak ke median)
set.seed(245)
vegan::permutest(permdisp_model)

Permutation test for homogeneity of multivariate dispersions
Permutation: free
Number of permutations: 999

Response: Distances
           Df  Sum Sq Mean Sq      F N.Perm Pr(>F)    
Groups      2  190082   95041 8.3286    999  0.001 ***
Residuals 175 1997003   11411                         
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

MANOVA untuk screening awal

model_manova <- manova(Y_matrix ~ Type, data = df)

parameters(model_manova,type=3,test="Pillai") %>% 
print_html()
Model Summary
Parameter df Statistic df (num.) df (error) F p
Type 2 1.71 26 328 73.15 < .001
Pillai test statistic Anova Table (Type 3 tests)

Artinya, secara statistik terdapat perbedaan profil komposisi kimiawi (vektor rata-rata multivariat) yang sangat signifikan di antara ketiga tipe anggur (variabel Type). Nilai Pillai’s Trace sebesar \(1.71\) juga tergolong sangat tinggi (mendekati nilai maksimum teoretisnya yaitu \(2\) untuk kasus \(3\) kelas), yang mengindikasikan bahwa daya pemisah antar kelas sangatlah kuat.

Uji MANOVA berfungsi sebagai ” alat deteksi. MANOVA telah menjawab pertanyaan: “Apakah ada perbedaan komposisi kimia antar tipe anggur?” dengan jawaban “Ya, sangat berbeda.”

Namun, MANOVA tidak bisa menjawab pertanyaan analitik dan prediktif selanjutnya. Di sinilah Analisis Diskriminan mengambil alih untuk dua tujuan utama:

Jika asumsi matriks kovarians antar kelas terpenuhi, LDA memungkinkan kita melakukan: 1. Feature Importance: Mengetahui variabel kimia apa saja yang paling berkontribusi membedakan ketiga tipe anggur tersebut melalui koefisien diskriminan. 2. Dimensionality Reduction & Visualisasi: Mereduksi dimensi data yang rumit ke dalam sebuah ruang grafik yang optimal (plot sumbu \(LD1\) vs \(LD2\)) agar pemisahan kelas bisa divisualisasikan secara jelas.

Jika kita memiliki sampel anggur baru yang belum diketahui tipenya, model LDA maupun QDA dapat menghitung peluang posterior untuk memprediksi anggur tersebut masuk ke kelas yang mana. Jika varians antar kelas terbukti berbeda (Box’s M / PERMDISP signifikan), maka QDA adalah pilihan yang lebih tepat khusus untuk tujuan prediksi ini.

Menyiapkan Pembagian Data

K-fold Cross Validation

K-fold Cross Validation adalah prosedur pengambilan sampel berulang yang melibatkan pembagian dataset menjadi K bagian yang sama besar atau hampir sama besar, yang disebut fold (lipatan). Ide dari metode ini adalah untuk training dan testing model klasifikasi sebanyak K kali, menggunakan fold(lipatan) yang berbeda sebagai testing data dalam setiap ulangan sambil menggunakan lipatan K-1 yang lain sebagai training data.

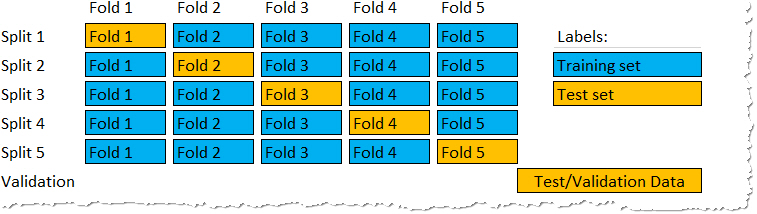
Pemilihan nilai K tergantung pada ukuran dataset dan trade-off antara waktu komputasi dan bias validasi. Nilai umum untuk K adalah 5 dan 10, tetapi kita dapat bereksperimen dengan nilai yang berbeda untuk menemukan keseimbangan terbaik untuk masalah spesifik.

set.seed(345)
folds <- vfold_cv(df, v = 10,strata = "Type" )

Mendefinisikan Model

Linear Discriminant

disc_linear <-  discrim_linear()%>% 
  set_engine(engine = "MASS") %>% 
  set_mode("classification")

Quadratic Discriminant

disc_quad <- discrim_quad() %>% 
              set_engine(engine = "MASS") %>% 
              set_mode("classification")

Mendefinisikan praproses data

Pendefinisikan praproses data dapat dilakukan dengan fungsi recipe.

basic_recipe <- recipe(Type~.,data =df)
basic_recipe 
── Recipe ──────────────────────────────────────────────────────────────────────
── Inputs 
Number of variables by role
outcome:    1
predictor: 13

Menggabungkan tahap praproses data dan model

models <- list(disc_linear=disc_linear,
               disc_quad =disc_quad)
preproc <- list(basic_recipe=basic_recipe)
wf_set <- workflow_set(preproc = preproc,models = models,
                       cross = TRUE)

Training Models

train_models <- workflow_map(wf_set,
                             fn="fit_resamples",
                            resamples = folds,
                            control=control_resamples(save_workflow = TRUE),
                            metrics=metric_set(sensitivity,
                                               specificity,
                                              bal_accuracy,
                                              f_meas),
                            seed = 2123)

Evaluasi Model

autoplot(train_models,type="wflow_id",
         rank_metric = "bal_accuracy")+
  scale_y_continuous(limits = c(0,1)) +
  theme_lares() +
  # memindahkan legend ke bawah
  theme(legend.position = "bottom")+
  # legend menjadi 2 baris
  guides(color = guide_legend(nrow = 2))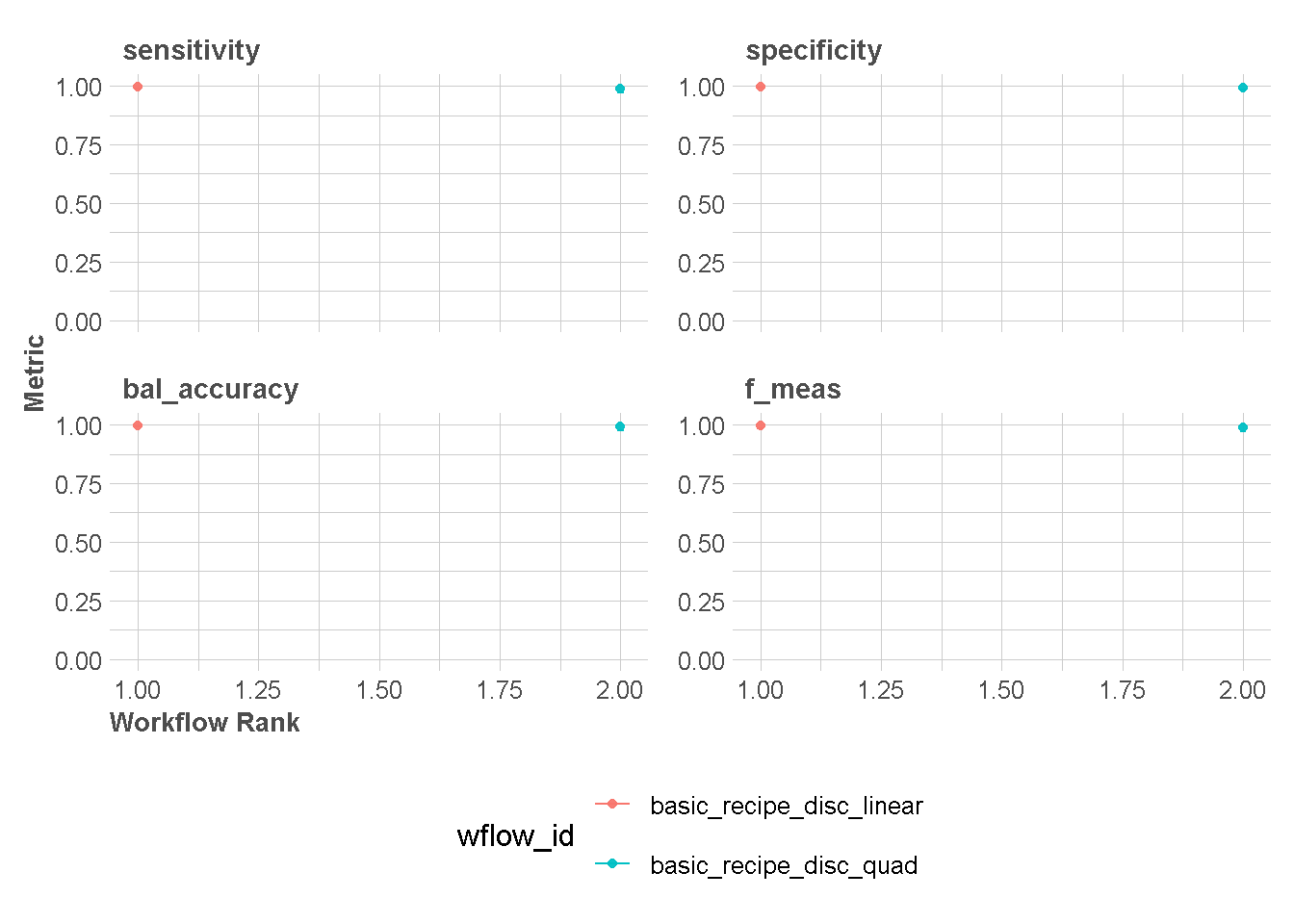

rank_results(train_models,rank_metric = "bal_accuracy") %>% 
  filter(.metric=="bal_accuracy") %>% 
  dplyr::select(wflow_id,.metric,mean,std_err,rank)
rank_results(train_models,rank_metric = "f_meas") %>% 
  filter(.metric=="f_meas") %>% 
  dplyr::select(wflow_id,.metric,mean,std_err,rank)

Menentukan Model terbaik dari Training

mod_best1 <- fit_best(x = train_models,metric = "bal_accuracy")
mod_best1
══ Workflow [trained] ══════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: discrim_linear()

── Preprocessor ────────────────────────────────────────────────────────────────
0 Recipe Steps

── Model ───────────────────────────────────────────────────────────────────────
Call:
lda(..y ~ ., data = data)

Prior probabilities of groups:
        1         2         3 
0.3314607 0.3988764 0.2696629 

Group means:
   Alcohol    Malic      Ash Alcalinity Magnesium  Phenols Flavanoids
1 13.74475 2.010678 2.455593   17.03729  106.3390 2.840169  2.9823729
2 12.27873 1.932676 2.244789   20.23803   94.5493 2.258873  2.0808451
3 13.15375 3.333750 2.437083   21.41667   99.3125 1.678750  0.7814583
  Nonflavanoids Proanthocyanins    Color       Hue Dilution   Proline
1      0.290000        1.899322 5.528305 1.0620339 3.157797 1115.7119
2      0.363662        1.630282 3.086620 1.0562817 2.785352  519.5070
3      0.447500        1.153542 7.396250 0.6827083 1.683542  629.8958

Coefficients of linear discriminants:
                         LD1           LD2
Alcohol         -0.403399781  0.8717930699
Malic            0.165254596  0.3053797325
Ash             -0.369075256  2.3458497486
Alcalinity       0.154797889 -0.1463807654
Magnesium       -0.002163496 -0.0004627565
Phenols          0.618052068 -0.0322128171
Flavanoids      -1.661191235 -0.4919980543
Nonflavanoids   -1.495818440 -1.6309537953
Proanthocyanins  0.134092628 -0.3070875776
Color            0.355055710  0.2532306865
Hue             -0.818036073 -1.5156344987
Dilution        -1.157559376  0.0511839665
Proline         -0.002691206  0.0028529846

Proportion of trace:
   LD1    LD2 
0.6875 0.3125

Interpretasi Model Terbaik

coefficient <- mod_best1 %>% 
  extract_fit_engine() %>% 
  coef() %>% 
  as.data.frame() %>% 
  rownames_to_column(var = "Predictors") 
coefficient
## custom function
lda_equation <-function(x,names){
  str_c(str_c("(",x,")",
                   names,collapse = "+"
                   )
        )
}
coefficient %>% 
  mutate(across(where(is.numeric),function(x) round(x,digits = 2))) %>%
  summarise(D1=lda_equation(LD1,Predictors),
            D2=lda_equation(LD2,Predictors)) %>% 
  pivot_longer(c(D1,D2),names_to = "discriminant",
               values_to="equation"
               )
## custom function
autoplot.lda<-function(object,response,data){
  object %>% 
  predict(newdata = data) %>% 
  magrittr::extract2("x") %>% 
  as_tibble() %>% 
  bind_cols(data %>% dplyr::select(all_of(response))) %>% 
ggscatter(x="LD1",y="LD2",color = response)
}
mod_best1 %>% 
  extract_fit_engine() %>% 
  autoplot(response="Type",data=df)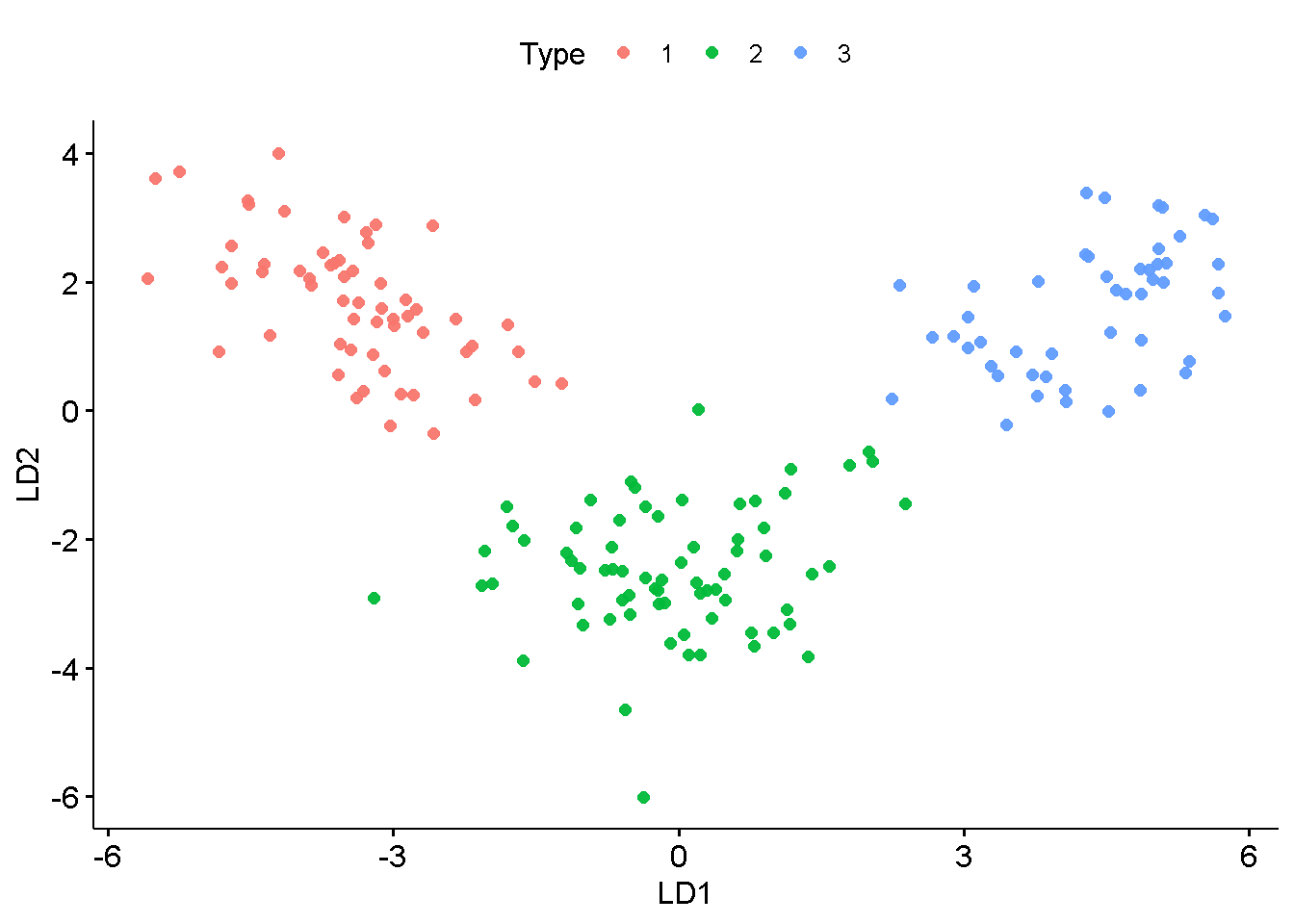

Prediksi Data baru

Berikut kita generate data baru dummy

set.seed(1234)
data_baru <- df %>% 
              slice_sample(n = 2,by = Type) %>% 
              dplyr::select(-Type)
data_baru
pred_data_baru1 <- mod_best1%>% 
                      predict(new_data = data_baru)
pred_data_baru1