Newton Raphson dan Fisher Scoring untuk Maximum Likelihood Estimation

Statistical Inference
Computational Statistics
Author

Gerry Alfa Dito

Published

September 1, 2023

Pengantar Newton Raphson

Metode Newton-Raphson adalah algoritme iteratif yang digunakan untuk menemukan akar-akar(roots) (roots finding) suatu fungsi. Metode ini pertama kali diperkenalkan oleh matematikawan Inggris, Isaac Newton, pada tahun 1685 dan kemudian disempurnakan oleh Joseph Raphson pada tahun 1690.

Akar-akar(roots) suatu fungsi tak linear (nonlinear) \(f(x)\) didefinisikan sebagai nilai \(x\) yang menyebabkan fungsi \(f\) memenuhi persamaan: \[ f(x)=0 \] Misal \[ f(x)=x^2+5x+6 \] maka nilai akar-akarnya adalah \(x=3\) atau \(x=2\)

Newton-Raphson dimulai dengan perkiraan awal (initial guess) nilai akar fungsi dan kemudian secara iteratif menyempurnakan perkiraan tersebut hingga mencapai akar yang sebenarnya. Pada setiap iterasi, Newton-Raphson ini menggunakan turunan fungsi untuk menghitung kemiringan garis singgung berdasarkan perikiraan nilai akar fungsi, Kemudian menetapkan perikiraan nilai akar fungsi berikutnya sebagai titik di mana garis singgung memotong sumbu \(x\).

Secara matematis proses iteratif ini dapat dituliskan: \[ x_{i+1} = x_i - \frac{f(x_i)}{f'(x_i)} \] dimana:

  • \(x_i\) adalah perkiraan nilai akar fungsi saat iterasi ke-i.

  • \(x_{i+1}\) adalah updating perkiraan nilai akar fungsi untuk iterasi selanjutnya (\(i + 1\)).

  • \(f(x_i)\) adalah nilai fungsi \(f(x)\) yang dievaluasi pada titik \(x_i\).

  • \(f'(x_i)\) adalah nilai turunan pertama dari fungsi \(f(x)\) yang dievaluasi pada titik \(x_i\).

  • \(f'(x_i)\) juga dapat dipandang sebagai nilai kemiringan (slope) garis singgung pada titik \(x_i\).

Secara grafis dapat diilustrasikan sebagai berikut

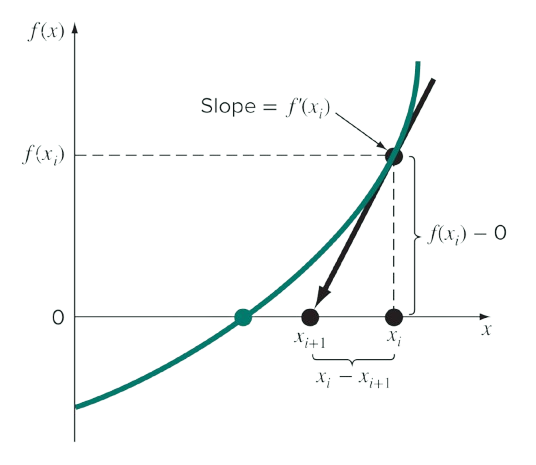
Algoritme Newton-Raphson

Algoritme Newton-Raphson untuk memperoleh akar-akar dari fungsi tak linear \(f(x)\) dapat dituliskan sebagai berikut:

  1. Tentukan perkiraan awal nilai akar fungsi \(x_0\) dan stopping criterion.

  2. Tentukan turunan pertama dari fungsi tak linear \(f(x)\) yaitu \(f'(x)\).

  3. Hitung \(x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}\), sehingga diperoleh perkiraan nilai akar fungsi \(x_1\).

  4. Lakukan Langkah 5 sampai stopping criterion terpenuhi.

  5. Hitung \(x_{i+1} = x_i - \frac{f(x_i)}{f'(x_i)}\) untuk iterasi \(i = 1, 2, \dots\)

  6. Saat stopping criterion terpenuhi maka \(x_{i+1}\) merupakan nilai akar fungsi untuk \(f(x)\).

Stopping criterion untuk Newton-Rapshon

Stopping criterion digunakan untuk menentukan kapan iterasi pada newton Raphson berhenti. Berikut beberapa stopping criterion untuk Newton Raphson:

  1. Banyaknya iterasi maksimum: Kriteria ini hanya menghentikan iterasi saat mencapai iterasi tertentu yang sudah ditentukan di awal. Keuntungannya adalah mudah diimplementasikan, namun kekuranganya adalah algoritme mungkin tidak konvergen dalam iterasi yang ditentukan.

  2. Absolute Error: Kriteria ini menghitung jarak antara perkiraan nilai akar fungsi \(x_i\) dan \(x_{i+1}\). Hasil perhitungan jarak ini harus kurang dari suatu nilai toleransi \(\epsilon\) agar proses iterasi berhenti (konvergen). Berikut adalah bentuk matematisnya \[|x_{(i+1)}-x_{i}| < \epsilon\]

  3. Relative Absolute Error: Kriteria ini menghitung jarak antara perkiraan nilai akar fungsi \(x_i\) dan \(x_{(i+1)}\) relatif pada perkiraan nilai akar fungsi \(x_i\). Hasil perhitungan jarak ini harus kurang dari suatu nilai toleransi \(\epsilon\) agar proses iterasi berhenti (konvergen). Berikut adalah bentuk matematisnya \[\frac{|x_{(i+1)}-x_{i}|}{x_{i}} < \epsilon\]

  4. Kriteria Kombinasi: Kriteria ini menggabungkan kriteria sebelumnya sehingga saling melengkapi satu sama lain.

Nilai tolerasi \(\epsilon\) dapat ditentukan sesuai dengan tingkat kepresisian nilai akar fungsi yang diperoleh terhadap nilai akar fungsi yang diperoleh

Newton-Rapshon untuk Masalah Optimisasi

Masalah penentuan akar-akar fungsi (roots finding) dan optimisasi saling berkaitan sebab keduanya melibatkan pencarian titik-titik pada suatu fungsi. Root finding mencari titik-titik (nilai \(x\)) yang menyebabkan fungsi \(f\) memenuhi persamaan \(f(x)=0\), sementara optimisasi mencari titik-titik (nilai\(x\)) yang menyebabkan fungsi \(f\) bernilai maksimum/minimum (optimal).

Berikut ilustrasi grafik perbedaan antara Root Finding dan optimisasi:

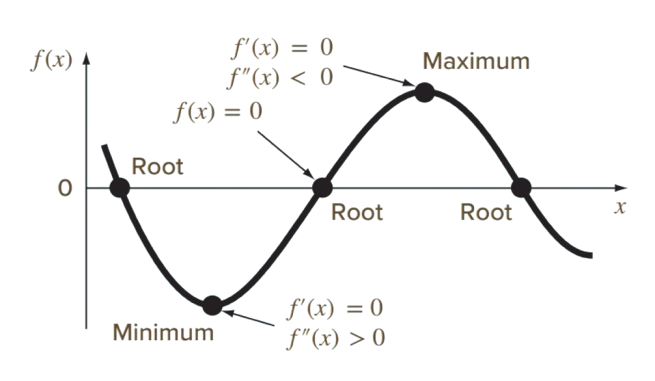
Berdasarkan grafik tersebut, ada beberapa hal yang perlu diperhatikan:

  • Secara matematis, titik optimal dari suatu fungsi \(f\) dapat dihitung dengan mencari nilai \(x\) sedemikian sehingga turunan pertama dari fungsi \(f\) bernilai nol atau \(f'(x) = 0\).

  • Jika turunan kedua dari fungsi \(f\) pada nilai \(x\) tersebut positif (\(f''(x) > 0\)) berarti nilai \(x\) tersebut merupakan nilai yang menyebabkan fungsi \(f\) minimum.

  • Jika turunan kedua dari fungsi \(f\) pada nilai \(x\) tersebut negatif (\(f''(x) < 0\)) berarti nilai \(x\) tersebut merupakan nilai yang menyebabkan fungsi \(f\) maksimum.

Kemudian,formula Newton-Raphson masalah optimisasi menjadi \[ x_{i+1} = x_i - \frac{f'(x_i)}{f''(x_i)} \qquad(1)\] dimana

  • \(x_i\) adalah perkiraan nilai akar fungsi saat iterasi ke-i

  • \(x_{i+1}\) adalah updating perkiraan nilai akar fungsi untuk iterasi selanjutnya \((i+1)\)

  • \(f'(x_i)\) adalah nilai turunan pertama dari fungsi \(f(x)\) yang dievaluasi pada titik \(x_i\)

  • \(f''(x_i)\) adalah nilai turunan kedua dari fungsi \(f(x)\) yang dievaluasi pada titik \(x_i\)

Formula Newton-Raphson pada Equation 1 digunakan untuk masalah optimisasi satu dimensi (one-dimensional)

Newton-Raphson juga dapat digunakan untuk masalah optimisasi multi dimensi (multi-dimensional). Optimisasi multi dimensi melibatkan fungsi multi-variabel \(f(x_1, x_2, \dots, x_p)\) sehingga nilai yang menyebabkan fungsi \(f\) maksimum/minimum berasal lebih dari \(p\) variabel.Optimisasi multi dimensi juga lebih mudah dinyatakan dalam bentuk vektor sehingga \(f(x) = f(x_1, x_2, \dots, x_p)\) dimana \(\boldsymbol{x} = \begin{bmatrix} x_1, x_2, \dots, x_p \end{bmatrix}^T\). Sehingga Metode Newton-Raphson untuk optimisasi multi dimensi dapat dituliskan sebagai berikut: \[ \boldsymbol{x}^{(i+1)} = \boldsymbol{x}^{(i)} - \frac{f'(\boldsymbol{x}^{(i)})}{f''(\boldsymbol{x}^{(i)})} \qquad(2)\] dengan

  • \(\boldsymbol{x} = \begin{bmatrix} x_1, x_2, \dots, x_p \end{bmatrix}^T\)
  • \(f'(\boldsymbol{x})\) merupakan matriks khusus yang dinamakan matriks Jacobian, dan \(f''(\boldsymbol{x})\) merupakan matriks khusus yang dinamakan matriks Hessian.

Matriks Jacobian untuk optimisasi multi dimensi didefinisikan sebagai matriks yang berisi turunan pertama parsial dari \(f(\boldsymbol{x})\). Secara matematis dapat ditulis

\[ J_f(\boldsymbol{x}) = \begin{bmatrix} \frac{\partial f(\boldsymbol{x})}{\partial x_1} \\ \frac{\partial f(\boldsymbol{x})}{\partial x_2} \\ \vdots \\ \frac{\partial f(\boldsymbol{x})}{\partial x_p} \end{bmatrix} \qquad(3)\]

Sementara itu, Matriks Hessian untuk optimisasi multi dimensi didefinisikan sebagai matriks yang berisi turunan kedua parsial dari \(f(\boldsymbol{x})\). Secara matematis dapat ditulis

\[ \boldsymbol{H}_f(\boldsymbol{x}) = \begin{bmatrix} \frac{\partial^2 f(\boldsymbol{x})}{\partial x_1^2} & \frac{\partial^2 f(\boldsymbol{x})}{\partial x_1 \partial x_2} & \dots & \frac{\partial^2 f(\boldsymbol{x})}{\partial x_1 \partial x_p} \\ \frac{\partial^2 f(\boldsymbol{x})}{\partial x_2 \partial x_1} & \frac{\partial^2 f(\boldsymbol{x})}{\partial x_2^2} & \dots & \frac{\partial^2 f(\boldsymbol{x})}{\partial x_2 \partial x_p} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f(\boldsymbol{x})}{\partial x_p \partial x_1} & \frac{\partial^2 f(\boldsymbol{x})}{\partial x_p \partial x_2} & \dots & \frac{\partial^2 f(\boldsymbol{x})}{\partial x_p^2} \end{bmatrix} \qquad(4)\]

Sehingga formula metode Newton-Raphson untuk optimisasi multi-dimensional menjadi \[ \boldsymbol{x}^{(i+1)} = \boldsymbol{x}^{(i)} - \left[\boldsymbol{H}_f(\boldsymbol{x}^{(i)})\right]^{-1} \boldsymbol{J}_f(\boldsymbol{x}^{(i)}) \qquad(5)\]

Formula Newton-Raphson pada Equation 5 hanya dapat diterapkan untuk masalah optimisasi tanpa kendala (unconstrained optimization). Algoritme Newton-Raphson untuk optimisasi multi-dimensional dapat dituliskan sebagai berikut:

  1. Tentukan perkiraan awal nilai optimal \(\boldsymbol{x}^{(0)} = \begin{bmatrix} x_1^{(0)}, x_2^{(0)}, \dots, x_p^{(0)} \end{bmatrix}^T\) dan stopping criterion.

  2. Tentukan matriks Jacobian dan Hessian.

  3. Hitung \(\boldsymbol{x}^{(1)} = \boldsymbol{x}^{(0)} - \left[\boldsymbol{H}_f(\boldsymbol{x}^{(0)})\right]^{-1} \boldsymbol{J}_f(\boldsymbol{x}^{(0)})\), sehingga diperoleh perkiraan nilai optimal \(\boldsymbol{x}^{(1)}\).

  4. Lakukan Langkah 5 sampai stopping criterion terpenuhi.

  5. Hitung \(\boldsymbol{x}^{(i+1)} = \boldsymbol{x}^{(i)} - \left[\boldsymbol{H}_f(\boldsymbol{x}^{(i)})\right]^{-1} \boldsymbol{J}_f(\boldsymbol{x}^{(i)})\) untuk iterasi \(i = 1, 2, \dots\)

  6. Saat stopping criterion terpenuhi maka \(\boldsymbol{x}^{(i+1)}\) merupakan nilai optimal fungsi untuk \(f(x)\).

Newton-Rapshon untuk Maximum Likelihood Estimation

Metode Newton-Raphson dapat digunakan untuk mendapatkan nilai dugaan parameter yang didasarkan pada proses pendugaan Maximum Likelihood Estimation (MLE). MLE memperoleh penduga bagi parameter \(\boldsymbol{\theta} = [\theta_1, \theta_2, \dots, \theta_p]\) dengan memaksimumkan fungsi log-likelihood \(l(\theta | x) = \log L(\theta | x)\), secara matematis dapat ditulis \[ \hat{\theta} = \arg \max_{\theta} l(\theta | x) \] MLE dapat dipandang sebagai masalah optimisasi multi dimensi, sehingga Newton-Raphson yang digunakan adalah Newton-Raphson untuk optimisasi multi dimensi. Matriks Jacobian pada Newton-Raphson untuk optimisasi multi dimensi dikenal dengan istilah score function untuk kasus ini. Sementara itu, Matriks Hessian dikenal sebagai Observed Fisher Information.

Score function didefinisikan sebagai:

\[ \begin{aligned} S(\boldsymbol{\theta}) &= J_f(\boldsymbol{\theta}) \\ &= \begin{bmatrix} \frac{\partial l(\boldsymbol{\theta} \mid x)}{\partial \theta_1} \\ \frac{\partial l(\boldsymbol{\theta} \mid x)}{\partial \theta_2} \\ \vdots \\ \frac{\partial l(\boldsymbol{\theta} \mid x)}{\partial \theta_p} \end{bmatrix} \\ &= \begin{bmatrix} S(\theta_1) \\ S(\theta_2) \\ \vdots \\ S(\theta_p) \end{bmatrix} \end{aligned} \qquad(6)\]

Kemudian Observed Fisher Information didefinisikan sebagai

\[ \begin{aligned} I(\boldsymbol{\theta}) &= -\boldsymbol{H}_f(\boldsymbol{\theta}) \\ &= - \begin{bmatrix} \frac{\partial^2 l(\boldsymbol{\theta} \mid x)}{\partial \theta_1^2} & \frac{\partial^2 l(\boldsymbol{\theta} \mid x)}{\partial \theta_1 \partial \theta_2} & \dots & \frac{\partial^2 l(\boldsymbol{\theta} \mid x)}{\partial \theta_1 \partial \theta_p} \\ \frac{\partial^2 l(\boldsymbol{\theta} \mid x)}{\partial \theta_2 \partial \theta_1} & \frac{\partial^2 l(\boldsymbol{\theta} \mid x)}{\partial \theta_2^2} & \dots & \frac{\partial^2 l(\boldsymbol{\theta} \mid x)}{\partial \theta_2 \partial \theta_p} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 l(\boldsymbol{\theta} \mid x)}{\partial \theta_p \partial \theta_1} & \frac{\partial^2 l(\boldsymbol{\theta} \mid x)}{\partial \theta_p \partial \theta_2} & \dots & \frac{\partial^2 l(\boldsymbol{\theta} \mid x)}{\partial \theta_p^2} \end{bmatrix} \\ &= - \begin{bmatrix} \frac{\partial S(\theta_1)}{\partial \theta_1} & \frac{\partial S(\theta_1)}{\partial \theta_2} & \dots & \frac{\partial S(\theta_1)}{\partial \theta_p} \\ \frac{\partial S(\theta_2)}{\partial \theta_1} & \frac{\partial S(\theta_2)}{\partial \theta_2} & \dots & \frac{\partial S(\theta_2)}{\partial \theta_p} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial S(\theta_p)}{\partial \theta_1} & \frac{\partial S(\theta_p)}{\partial \theta_2} & \dots & \frac{\partial S(\theta_p)}{\partial \theta_p} \end{bmatrix} \end{aligned} \qquad(7)\]

Sehingga formulasi Newton-Raphson untuk MLE adalah sebagai berikut

\[ \begin{aligned} \boldsymbol{\theta}^{(i+1)} &= \boldsymbol{\theta}^{(i)} - \left[ \boldsymbol{H}_f\left(\boldsymbol{\theta}^{(i)}\right) \right]^{-1} \boldsymbol{J}_f\left(\boldsymbol{\theta}^{(i)}\right) \\ &= \boldsymbol{\theta}^{(i)} - \left[ -\boldsymbol{I}\left(\boldsymbol{\theta}^{(i)}\right) \right]^{-1} \boldsymbol{S}\left(\boldsymbol{\theta}^{(i)}\right) \\ &= \boldsymbol{\theta}^{(i)} + \left[ \boldsymbol{I}\left(\boldsymbol{\theta}^{(i)}\right) \right]^{-1} \boldsymbol{S}\left(\boldsymbol{\theta}^{(i)}\right) \end{aligned} \] ,yang secara lengkap dapat dituliskan

\[ \begin{aligned} \boldsymbol{\theta}^{(i+1)} &= \boldsymbol{\theta}^{(i)} + \left[ \boldsymbol{I}\left(\boldsymbol{\theta}^{(i)}\right) \right]^{-1} \boldsymbol{S}\left(\boldsymbol{\theta}^{(i)}\right) \end{aligned} \qquad(8)\]

dengan

  • \(\boldsymbol{\theta} = \begin{bmatrix} \theta_1, \theta_2, \dots, \theta_p \end{bmatrix}^T\)

  • \(\boldsymbol{J}_f\left(\boldsymbol{\theta}^{(i)}\right)\) adalah matriks Jacobian untuk perkiraan parameter dugaan \(\boldsymbol{\theta}^{(i)}\).

  • \(\boldsymbol{H}_f\left(\boldsymbol{\theta}^{(i)}\right)\) adalah matriks Hessian untuk perkiraan parameter dugaan \(\boldsymbol{\theta}^{(i)}\).

  • \(\boldsymbol{S}\left(\boldsymbol{\theta}^{(i)}\right)\) adalah Score function untuk perkiraan parameter dugaan \(\boldsymbol{\theta}^{(i)}\).

  • \(\boldsymbol{I}\left(\boldsymbol{\theta}^{(i)}\right)\) adalah Observed Fisher Information untuk perkiraan parameter dugaan \(\boldsymbol{\theta}^{(i)}\).

Fisher Scoring

Metode Fisher-Scoring merupakan Metode Newton-Raphson yang diterapkan pada MLE dengan mengganti komponen Observed Fisher Information dengan Expected Fisher Information. Expected Fisher Information didefinisikan sebagai:

\[ \mathcal{I}(\theta) = E_\theta \left( I(\theta) \right) = -E\left( \mathbf{H}_f(\theta) \right) \]

Penggantian ini dikarenakan Expected Fisher Information, \(\mathcal{I}(\theta)\), memiliki keuntungan yaitu nilai-nilai \(\mathcal{I}(\theta)\) berdasarkan informasi pada populasi, sementara \(I(\theta)\) hanya menggunakan data contoh (sample). Sehingga nilai \(\mathcal{I}(\theta)\) tidak bergantung pada data yang diperoleh. Expected Fisher Information juga menyebabkan metode fisher scoring lebih cepat konvergen dibandingkan Newton-Raphson.

Lebih lengkap Expected Fisher Information didefinisikan sebagai:

\[ \begin{aligned} \mathcal{I}(\boldsymbol{\theta}) &= E_\theta \left( I(\boldsymbol{\theta}) \right) \\ &= E \left( -\mathbf{H}_f(\boldsymbol{\theta}) \right) \\ &= -E \left( \mathbf{H}_f(\boldsymbol{\theta}) \right) \\ &= - \begin{bmatrix} E \left( \frac{\partial^2 l(\boldsymbol{\theta} | x)}{\partial \theta_1^2} \right) & E \left( \frac{\partial^2 l(\boldsymbol{\theta} | x)}{\partial \theta_1 \partial \theta_2} \right) & \dots & E \left( \frac{\partial^2 l(\boldsymbol{\theta} | x)}{\partial \theta_1 \partial \theta_p} \right) \\ E \left( \frac{\partial^2 l(\boldsymbol{\theta} | x)}{\partial \theta_2 \partial \theta_1} \right) & E \left( \frac{\partial^2 l(\boldsymbol{\theta} | x)}{\partial \theta_2^2} \right) & \dots & E \left( \frac{\partial^2 l(\boldsymbol{\theta} | x)}{\partial \theta_2 \partial \theta_p} \right) \\ \vdots & \vdots & \ddots & \vdots \\ E \left( \frac{\partial^2 l(\boldsymbol{\theta} | x)}{\partial \theta_p \partial \theta_1} \right) & E \left( \frac{\partial^2 l(\boldsymbol{\theta} | x)}{\partial \theta_p \partial \theta_2} \right) & \dots & E \left( \frac{\partial^2 l(\boldsymbol{\theta} | x)}{\partial \theta_p^2} \right) \end{bmatrix} \end{aligned} \] Sehingga formulasi Fisher Scoring adalah sebagai berikut

\[ \begin{aligned} \boldsymbol{\theta}^{(i+1)} &= \boldsymbol{\theta}^{(i)} + \left[ \mathcal{I}\left(\boldsymbol{\theta}^{(i)}\right) \right]^{-1} \boldsymbol{S}\left(\boldsymbol{\theta}^{(i)}\right) \end{aligned} \qquad(9)\]

dengan

  • \(\boldsymbol{\theta} = \begin{bmatrix} \theta_1, \theta_2, \dots, \theta_p \end{bmatrix}^T\)

  • \(\boldsymbol{J}_f\left(\boldsymbol{\theta}^{(i)}\right)\) adalah matriks Jacobian untuk perkiraan parameter dugaan \(\boldsymbol{\theta}^{(i)}\).

  • \(\boldsymbol{H}_f\left(\boldsymbol{\theta}^{(i)}\right)\) adalah matriks Hessian untuk perkiraan parameter dugaan \(\boldsymbol{\theta}^{(i)}\).

  • \(\boldsymbol{S}\left(\boldsymbol{\theta}^{(i)}\right)\) adalah Score function untuk perkiraan parameter dugaan \(\boldsymbol{\theta}^{(i)}\).

  • \(\mathcal{I}\left(\boldsymbol{\theta}^{(i)}\right)\) adalah Observed Fisher Information untuk perkiraan parameter dugaan \(\boldsymbol{\theta}^{(i)}\).