install.packages("see")Regresi logistik dengan R
Package
library(tidyverse)
library(broom)
library(broom.helpers)
library(skimr)
library(performance)
library(rsample)
library(yardstick)
library(DataExplorer)Sebenarnya Anda tidak perlu untuk load keseluruhan pakcage, Anda bisa menggunakan syntax namapackage::fungsi untuk menggunakan suatu fungsi dari suatu package di R, selama package tersebut sudah Anda Install.
Data
Data ini terkait dengan promosi marketing langsung dari suatu institusi perbankan Portugal. Promosi marketing tersebut didasarkan pada panggilan telepon. Sering kali, diperlukan lebih dari satu kali kontak ke klien yang sama, untuk memastikan apakah produk (deposito berjangka bank) akan (atau tidak) berlangganan.
| No | Variabel | Keterangan |
|---|---|---|
| 1 | age | umur nasabah(numeric) |
| 2 | job | jenis pekerjaan nasabah(categorical:"admin.","unknown","unemployed","management","housemaid","entrepreneur","student","blue-collar","self-employed","retired","technician","services") |
| 3 | marital | status perkawinan nasabah (categorical: "married","divorced","single") |
| 4 | education | tingkat pendidikan(categorical: "unknown","secondary","primary","tertiary") |
| 5 | default | apakah nasabah memiliki kredit yang macet? (binary: "yes","no") |
| 6 | balance | saldo tahunan rata-rata dalam euros (numeric) |
| 7 | housing | apakah nasabah memiliki cicilan rumah? (binary: "yes","no") |
| 8 | loan | apakah nasabah memiliki pinjaman pribadi? (binary: "yes","no") |
| 9 | contact | perangkat telekomunikasi (categorical: "unknown","telephone","cellular") |
| 10 | duration | durasi panggilan terakhir, dalam detik (numeric) |
| 11 | pdays | banyaknya hari yang telah berlalu setelah klien terakhir kali dihubungi dari campaign sebelumnya (angka, -1 berarti klien tidak dihubungi sebelumnya) |
| 12 | previous | banyaknya komunikasi yang dilakukan sebelum campaign ini(numeric) |
| 13 | poutcome | hasil dari promosi campaign sebelumnya (categorical: "unknown","other","failure","success") |
| 14 | subscribed | response variable (desired target),apakah nasabah telah berlangganan deposito berjangka? (binary: "yes","no") |
Import Data
bank_marketing <- read_csv("bank_marketing.csv")Rows: 45211 Columns: 14
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (9): subscribed, job, marital, education, default, housing, loan, contac...
dbl (5): age, balance, duration, pdays, previous
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.glimpse(bank_marketing)Rows: 45,211
Columns: 14
$ subscribed <chr> "no", "no", "no", "no", "no", "no", "no", "no", "no", "no",…
$ age <dbl> 58, 44, 33, 47, 33, 35, 28, 42, 58, 43, 41, 29, 53, 58, 57,…
$ job <chr> "management", "technician", "entrepreneur", "blue-collar", …
$ marital <chr> "married", "single", "married", "married", "single", "marri…
$ education <chr> "tertiary", "secondary", "secondary", "unknown", "unknown",…
$ default <chr> "no", "no", "no", "no", "no", "no", "no", "yes", "no", "no"…
$ balance <dbl> 2143, 29, 2, 1506, 1, 231, 447, 2, 121, 593, 270, 390, 6, 7…
$ housing <chr> "yes", "yes", "yes", "yes", "no", "yes", "yes", "yes", "yes…
$ loan <chr> "no", "no", "yes", "no", "no", "no", "yes", "no", "no", "no…
$ contact <chr> "unknown", "unknown", "unknown", "unknown", "unknown", "unk…
$ duration <dbl> 261, 151, 76, 92, 198, 139, 217, 380, 50, 55, 222, 137, 517…
$ pdays <dbl> -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,…
$ previous <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ poutcome <chr> "unknown", "unknown", "unknown", "unknown", "unknown", "unk…karena fungsi glm untuk membutuhkan semua variabel (kolom) kategorik (biner atau nominal) dalam tipe data factor maka kita akan konversi terlebih dahulu.
bank_marketing <- bank_marketing %>%
mutate(across(where(is.character),.fns =as.factor))
glimpse(bank_marketing)Rows: 45,211
Columns: 14
$ subscribed <fct> no, no, no, no, no, no, no, no, no, no, no, no, no, no, no,…
$ age <dbl> 58, 44, 33, 47, 33, 35, 28, 42, 58, 43, 41, 29, 53, 58, 57,…
$ job <fct> management, technician, entrepreneur, blue-collar, unknown,…
$ marital <fct> married, single, married, married, single, married, single,…
$ education <fct> tertiary, secondary, secondary, unknown, unknown, tertiary,…
$ default <fct> no, no, no, no, no, no, no, yes, no, no, no, no, no, no, no…
$ balance <dbl> 2143, 29, 2, 1506, 1, 231, 447, 2, 121, 593, 270, 390, 6, 7…
$ housing <fct> yes, yes, yes, yes, no, yes, yes, yes, yes, yes, yes, yes, …
$ loan <fct> no, no, yes, no, no, no, yes, no, no, no, no, no, no, no, n…
$ contact <fct> unknown, unknown, unknown, unknown, unknown, unknown, unkno…
$ duration <dbl> 261, 151, 76, 92, 198, 139, 217, 380, 50, 55, 222, 137, 517…
$ pdays <dbl> -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1,…
$ previous <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,…
$ poutcome <fct> unknown, unknown, unknown, unknown, unknown, unknown, unkno…Eksplorasi Data
Menggunakan Ringkasan Statistik
skim_without_charts(data = bank_marketing)| Name | bank_marketing |
| Number of rows | 45211 |
| Number of columns | 14 |
| _______________________ | |
| Column type frequency: | |
| factor | 9 |
| numeric | 5 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| subscribed | 0 | 1 | FALSE | 2 | no: 39922, yes: 5289 |
| job | 0 | 1 | FALSE | 12 | blu: 9732, man: 9458, tec: 7597, adm: 5171 |
| marital | 0 | 1 | FALSE | 3 | mar: 27214, sin: 12790, div: 5207 |
| education | 0 | 1 | FALSE | 4 | sec: 23202, ter: 13301, pri: 6851, unk: 1857 |
| default | 0 | 1 | FALSE | 2 | no: 44396, yes: 815 |
| housing | 0 | 1 | FALSE | 2 | yes: 25130, no: 20081 |
| loan | 0 | 1 | FALSE | 2 | no: 37967, yes: 7244 |
| contact | 0 | 1 | FALSE | 3 | cel: 29285, unk: 13020, tel: 2906 |
| poutcome | 0 | 1 | FALSE | 4 | unk: 36959, fai: 4901, oth: 1840, suc: 1511 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 |
|---|---|---|---|---|---|---|---|---|---|
| age | 0 | 1 | 40.94 | 10.62 | 18 | 33 | 39 | 48 | 95 |
| balance | 0 | 1 | 1362.27 | 3044.77 | -8019 | 72 | 448 | 1428 | 102127 |
| duration | 0 | 1 | 258.16 | 257.53 | 0 | 103 | 180 | 319 | 4918 |
| pdays | 0 | 1 | 40.20 | 100.13 | -1 | -1 | -1 | -1 | 871 |
| previous | 0 | 1 | 0.58 | 2.30 | 0 | 0 | 0 | 0 | 275 |
Menggunakan Visualisasi
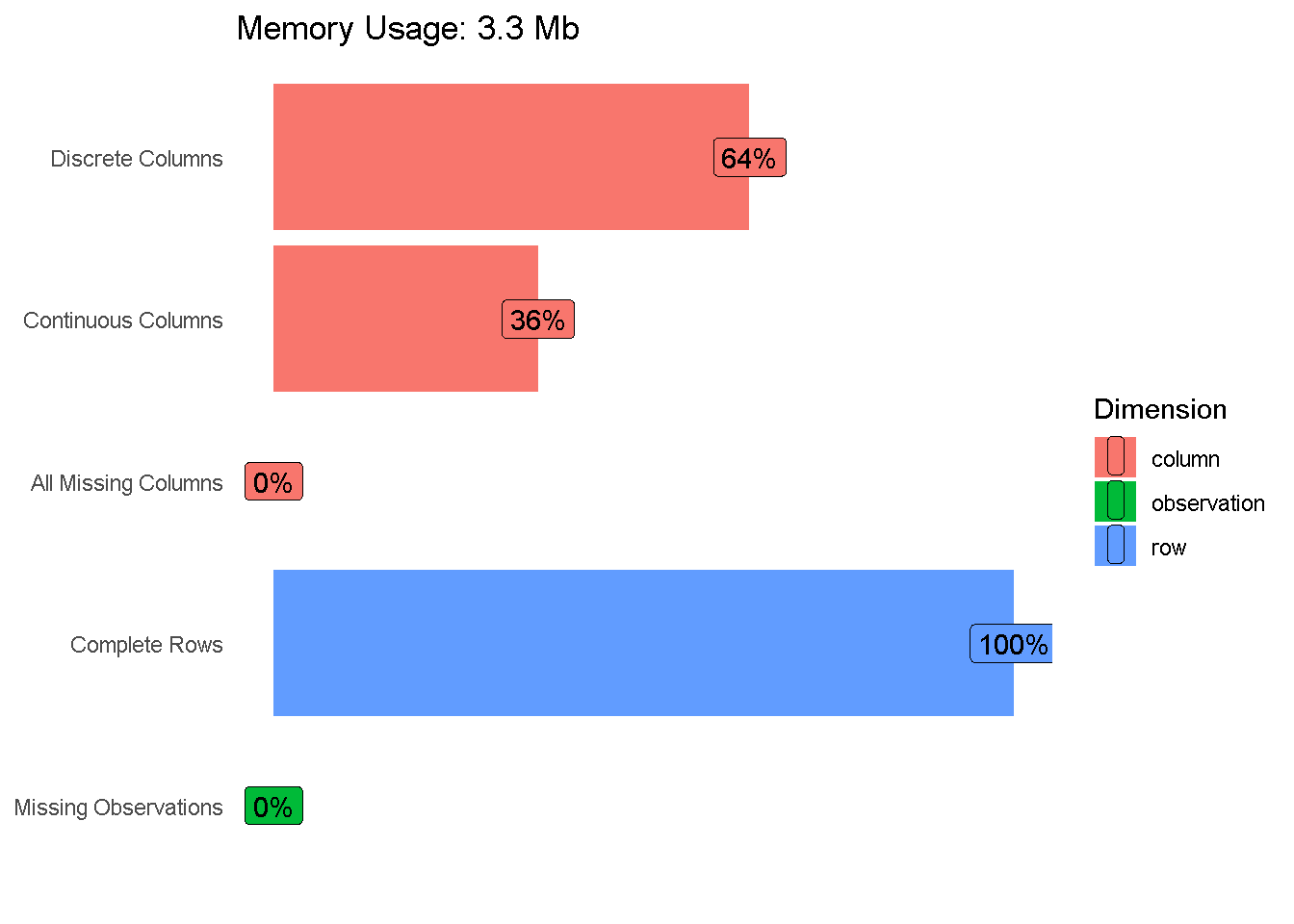
Eksplorasi Umum
plot_intro(data = bank_marketing,
ggtheme = theme_classic(),
theme_config = list(axis.line=element_blank(),
axis.ticks=element_blank(),
axis.text.x=element_blank(),
axis.title=element_blank()
)
)
Eksplorasi Korelasi
Korelasi variabel prediktor numerik dengan variabel response
plot_boxplot(data = bank_marketing,by = "subscribed",
geom_boxplot_args = list(fill="#03A9F4"),
ggtheme = theme_classic())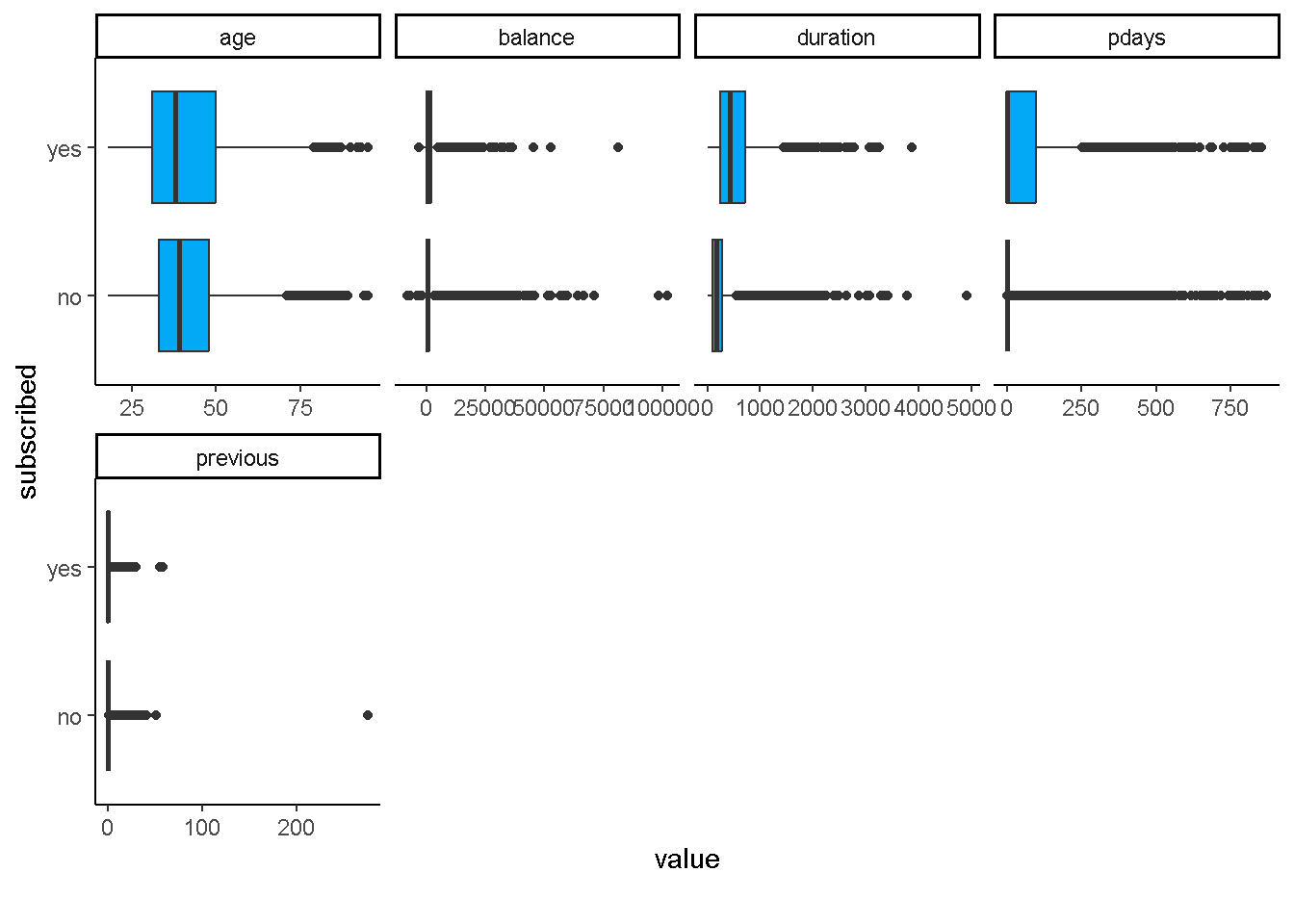
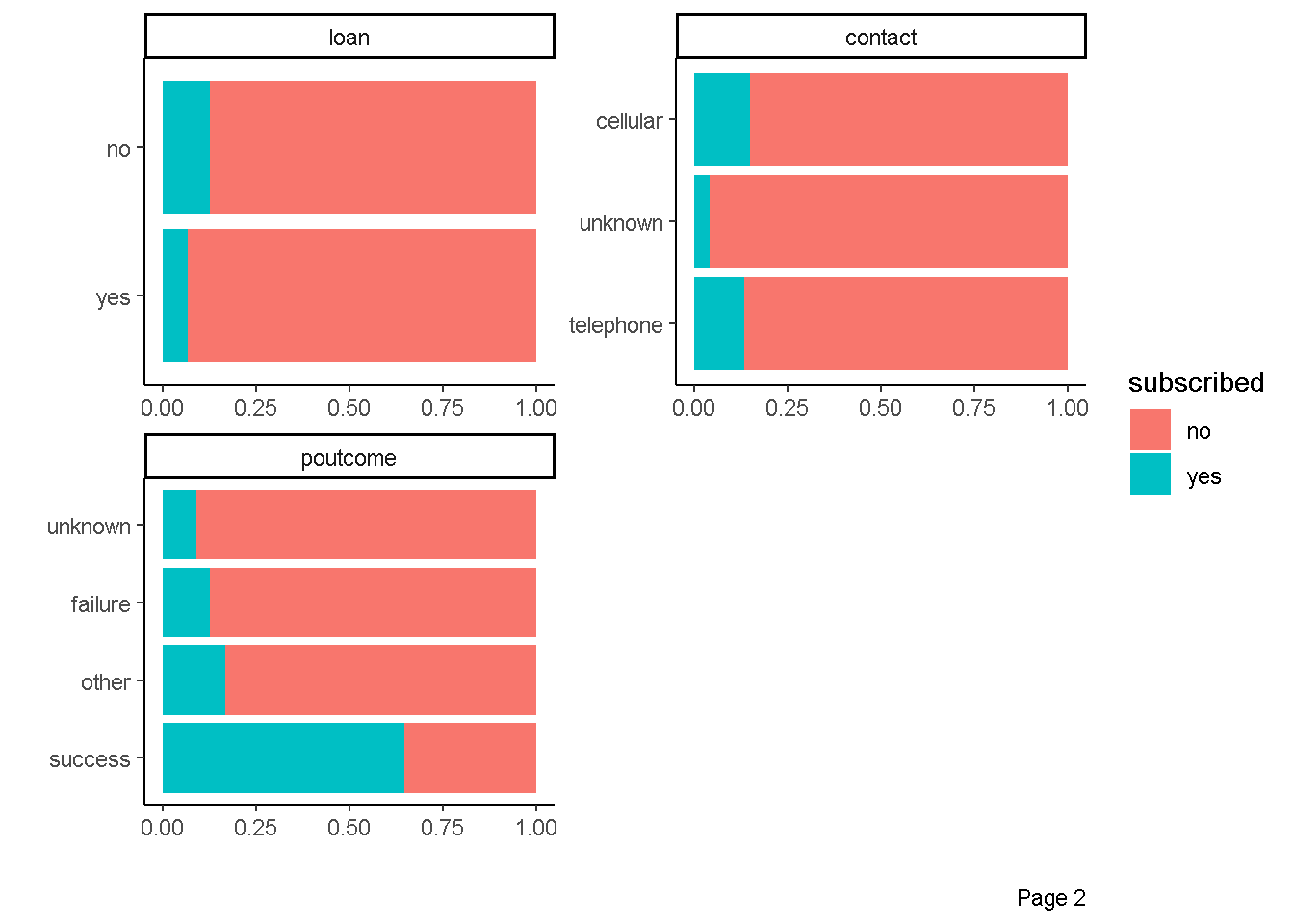
Korelasi variabel prediktor kategorik dengan variabel response
plot_bar(data = bank_marketing,by = "subscribed",
ggtheme = theme_classic(),
ncol = 2)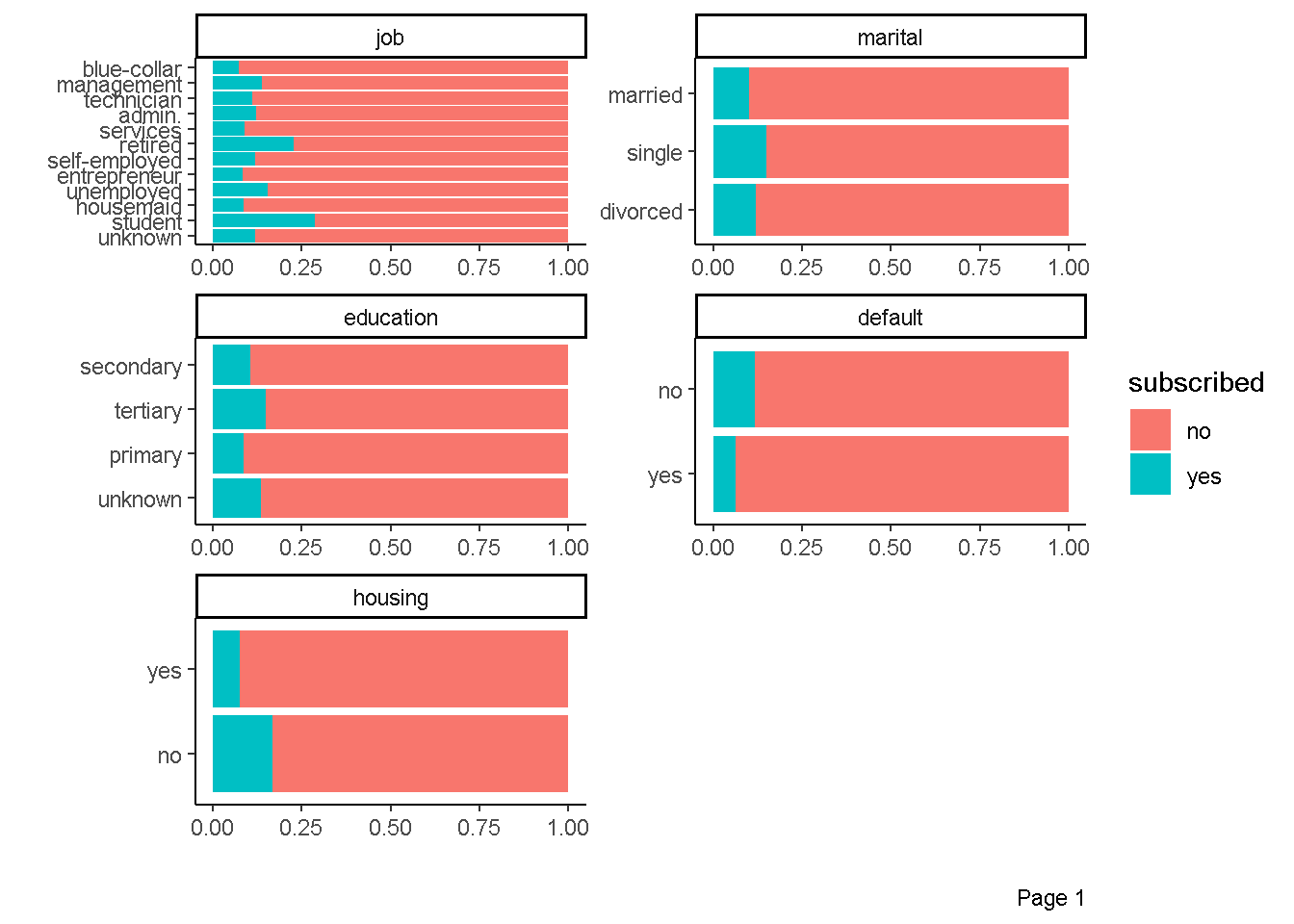
Pemodelan Regresi Logistik
Regresi Logistik Sederhana dengan variabel prediktor biner
Secara umum model regresi logistik sederhana dapat ditulis:
\[ \mathbf{\mu}=E(\textbf{y})=\log{\left[\frac{\pi(\textbf{x})}{1-\pi(\textbf{x})}\right]} = \beta_{0}+\beta_{1}\textbf{x} \]
dimana:
- \(\pi(\textbf{x})=P(Y=1|\pi(\textbf{x}))\) dan \(1-\pi(\textbf{x})=1-P(Y=1|\pi(\textbf{x}))=P(Y=0|\pi(\textbf{x}))\)
atau dapat juga ditulis
\[ \pi(\textbf{x}) = \frac{\exp{(\beta_{0}+\beta_{1}\textbf{x})}}{1+\exp{(\beta_{0}+\beta_{1}\textbf{x})}} \]
Pemodelan Regresi Logistik Sederhana dengan variabel prediktor biner perlu memperhatikan reference category atau kategori pembanding dari variabel prediktor biner tersebut. Kategori pembanding akan dikodekan dengan 0 dan kategori lainnya akan dikodekan dengan 1. Proses pengkodean ini sebenarnya adalah proses transformasi variabel biner menjadi variabel numerik. Variable hasil transformasi ini sering disebut dengan variabel dummy atau variabel yang amtan-amatannya hanya bernilai 1 atau 0.
Dalam R, Kategori pembanding ini biasanya merupakan kategori pertama yang ditunjukkan dari output fungsi levels. Berikut ilustrasinya
levels(bank_marketing$housing)[1] "no" "yes"Berdasarkan output diatas, berarti Kategori pembanding-nya adalah "no" karena berada di urutan pertama. kita bisa merubah Kategori pembanding dengan fungsi relevel dan mengisi argumen ref dengan kategori yang akan dijadikan sebagai kategori pembanding. Berikut ilustrasinya
coba <- relevel(x = bank_marketing$housing,ref = "yes")
levels(coba)[1] "yes" "no" Kita bisa membandingkan proses transformasi variabel biner menjadi numerik 0 dan 1 menggunakan fungsi contrast
contrasts(bank_marketing$housing) %>% as.data.frame()contrasts(coba) %>% as.data.frame()fungsi glm dapat digunakan untuk menjalan regresi logistik.
mod1 <-glm(subscribed=="yes"~housing,data=bank_marketing,family=binomial(link = "logit"))- sintaks
subscribed=="yes"berarti kita menenetapkan kelas positifnya adalahyesatau \(P(Y=1|\pi(\textbf{x}))\) sedangkan kelas negatifnya adalahnoatau \(P(Y=0|\pi(\textbf{x}))\) - jika kita tidak mendefinisikan dengan sintaks
subscribed=="yes"maka secara default yang akan menjadi kelas positif adalah kategori pertama yang ditunjukkan dari output fungsilevels. Dalam kasus variabel responsubscribed, secara default yang menjadi kelas positif adalahno. Berikut cara mengecek kategori pertama darilevels.
levels(bank_marketing$subscribed)[1] "no" "yes"- sintaks
~housingmenandakan bahwahousingadalah variabel prediktor. - sintaks
family(link = "logit")digunakan untuk menandakan kita menggunakan regresi logistik.
kemudian untuk mengeluarkan nilai dugaan koefisien, Selang kepercayaan (Confidence Interval) dan p-value dapat menggunakan fungsi parameters dari package parameters
tidy_parameters(mod1,conf.int = TRUE,conf.level = 0.95,ci_method="wald")- Koefisien dari prediktor
housing [yes]\((\beta_{1})\) adalah \(-0.88\) (negatif) berarti saat nasabah memiliki cicilan rumah maka kemungkinan nasabah tidak akan berlangganan deposito berjangka. - Intercept \(\beta_{0}\) umumnya dapat diinterpretasikan dengan melakukan transformasi terlebih dahulu ke dalam bentuk peluang dengan mengatur nilai peubah prediktor sama dengan 0. Perhitungan ini bisa menggunakan fungsi
predictdan argumen daripredictyaitutype="response". - \(\text{p-value} = 0.001 < 0.05 = \alpha\) untuk prediktor
housing [yes]yang berarti sudah cukup bukti untuk menolak \(H_{0}: \beta_{1}=0\) yang berartihousing [yes]berpengaruh terhadapsubscribed. - 95% CI untuk \((\beta_{1})\) dapat diinterpretasikan jika sudah kita transformasi ke dalam Odd-Ratio
Untuk mendapatkan nilai Odds-Ratio dari koefisien dan intercept kita dapat menerapkan rumus berikut
\[ \text{Odds-Ratio}(\beta)=\exp{(\beta)} \]
sehingga
# intercept
exp(-1.61)[1] 0.1998876# koefisien
exp(-0.88)[1] 0.4147829atau lebih mudah jika kita menggunakan argumen exponentiate = TRUE pada fungsi parameters. Selain nilai koefisien dan intercept berubah menjadi Odds-Ratio, nilai standard error dan selang kepercayaan (CI) koefisien juga berubah menyesuaikan. Namun, nilai statistik z dan p-value tidak berubah.
tidy_parameters(mod1,conf.int = TRUE,conf.level = 0.95,ci_method="wald",exponentiate = TRUE) %>%
mutate(across(where(is.numeric),function(x) round(x,2) ))- Odds-Ratio dari prediktor
housing [yes]\((\beta_{1})\) adalah \(0.42\) berarti nasabah yang memiliki cicilan rumah mempunyai odds 58% \(([1-0.42]\times 100\%=0.58\times 100\%=58\%)\) lebih rendah dibandingkan dengan nasabah yang tidak memiliki cicilan rumah untuk berlangganan deposito berjangka. - 95% CI dari Odds-Ratio
housing [yes]berarti 95% yakin bahwa nasabah yang memiliki cicilan rumah menpunyai odds 56% sampai 61% lebih rendah dibandingkan dengan nasabah yang tidak memiliki cicilan rumah untuk berlangganan deposito berjangka - Peluang dari intercept \((\beta_{1})\) adalah
predict(object = mod1,newdata = data.frame(housing="no"),type = "response") 1
0.1670236 dapat diperhatikan bahwa nilai 0 pada prediktor housing adalah saat housing="no". Jadi, peluang nasabah yang tidak memiliki cicilan rumah untuk berlangganan deposito berjangka adalah \(0.1670236\). Secara matematis dapat dihitung sebagai berikut:
\[ \begin{eqnarray} \pi(\textbf{x}) &=& \frac{\exp{(\beta_{0}+\beta_{1}\textbf{x})}}{1+\exp{(\beta_{0}+\beta_{1}\textbf{x})}} \\ &=& \frac{\exp{(-1.61-0.88\textbf{x})}}{1+\exp{(-1.61-0.88\textbf{x})}} \\ \pi(0)&=& \frac{\exp{(-1.61-0.88[0])}}{1+\exp{(-1.61-0.88[0])}} \\ &=& \frac{\exp{(-1.61)}}{1+\exp{(-1.61)}} \\ &=& \frac{0.1998876}{1.199888} \\ &=& 0.1665886 \end{eqnarray} \]
Selanjutnya, kita coba mengubah kategori pembanding dari housing
bank_marketing2 <- bank_marketing %>%
mutate(housing=relevel(x=housing,ref="yes"))mod12 <-glm(subscribed=="yes"~housing,data=bank_marketing2,family=binomial(link = "logit"))tidy_parameters(mod12,conf.int = TRUE,conf.level = 0.95,ci_method="wald")tidy_parameters(mod12,conf.int = TRUE,conf.level = 0.95,ci_method="wald",exponentiate = TRUE) %>%
mutate(across(where(is.numeric),function(x) round(x,2) ))- Odds-Ratio dari prediktor
housing [no]\((\beta_{1})\) adalah \(2.40\) berarti nasabah yang tidak memiliki cicilan rumah mempunyai odds 140% \(([2.40-1]\times 100\%=1.4\times 100\%=140\%)\) lebih tinggi dibandingkan dengan nasabah yang memiliki cicilan rumah untuk berlangganan deposito berjangka.
Regresi Logistik Sederhana dengan variabel prediktor numerik
mod2 <-glm(subscribed~duration,data=bank_marketing,family=binomial(link = "logit"))kemudian untuk mengeluarkan nilai dugaan koefisien, Selang kepercayaan (Confidence Interval) dan p-value dapat menggunakan fungsi parameters dari package parameters
tidy_parameters(mod2,conf.int = TRUE,conf.level = 0.95,ci_method="wald")- Koefisien dari prediktor
duration\((\beta_{1})\) adalah \(-0.004\) (negatif) berarti semakin lama durasi panggilan terakhir maka semakin kecil kemungkinan nasabah untuk berlangganan deposito berjangka. - \(\text{p-value} = 0.001 < 0.05 = \alpha\) berarti sudah cukup bukti untuk menolak \(H_{0}: \beta_{1}=0\) yang berarti
durationberpengaruh terhadapsubscribed.
tidy_parameters(mod2,conf.int = TRUE,conf.level = 0.95,ci_method="wald",exponentiate = TRUE) %>%
mutate(across(where(is.numeric),function(x) round(x,2) ))- Odds-Ratio dari prediktor
duration\((\beta_{1})\) adalah \(1.00\) berarti semakin lama durasi panggilan terakhir maka semakin kecil kemungkinan nasabah untuk berlangganan deposito berjangka.
Regresi Logistik Berganda dengan variabel prediktor kategorik nominal
Secara umum model regresi logistik berganda dapat ditulis:
\[ \mathbf{\mu}=E(\textbf{y})=\log{\left[\frac{\pi(\textbf{X})}{1-\pi(\textbf{X})}\right]} = \beta_{0}+\beta_{1}\textbf{x}_{1}+\beta_{2}\textbf{x}_{2} +\ldots+\beta_{p}\textbf{x}_{p} \]
atau dapat juga ditulis
\[ \mathbf{\mu}=E(\textbf{y})=\log{\left[\frac{\pi(\textbf{X})}{1-\pi(\textbf{X})}\right]} =\textbf{X}\beta \]
\[ \pi(\textbf{X}) = \frac{\exp{(\textbf{X}\beta)}}{1+\exp{(\textbf{X}\beta)}} \]
Sama seperti variable prediktor kategorik biner, hal yang harus diperhatikan adalah kategori pembanding dari variabel prediktor kategorik nominal. kita bisa memeriksa kategori mana yang menjadi kategori pembanding dengan menggunakan fungsi levels
levels(bank_marketing$job) [1] "admin." "blue-collar" "entrepreneur" "housemaid"
[5] "management" "retired" "self-employed" "services"
[9] "student" "technician" "unemployed" "unknown" Berdasarkan output diatas kategori pembanding-nya adalah "admin.". Kita bisa melihat proses transformasi variabel nominal menjadi numerik 0 dan 1 menggunakan fungsi contrast
contrasts(bank_marketing$job) blue-collar entrepreneur housemaid management retired
admin. 0 0 0 0 0
blue-collar 1 0 0 0 0
entrepreneur 0 1 0 0 0
housemaid 0 0 1 0 0
management 0 0 0 1 0
retired 0 0 0 0 1
self-employed 0 0 0 0 0
services 0 0 0 0 0
student 0 0 0 0 0
technician 0 0 0 0 0
unemployed 0 0 0 0 0
unknown 0 0 0 0 0
self-employed services student technician unemployed unknown
admin. 0 0 0 0 0 0
blue-collar 0 0 0 0 0 0
entrepreneur 0 0 0 0 0 0
housemaid 0 0 0 0 0 0
management 0 0 0 0 0 0
retired 0 0 0 0 0 0
self-employed 1 0 0 0 0 0
services 0 1 0 0 0 0
student 0 0 1 0 0 0
technician 0 0 0 1 0 0
unemployed 0 0 0 0 1 0
unknown 0 0 0 0 0 1Berdasarkan output diatas, terlihat bahwa label pada baris menandakan kategori asal, sedangkan label pada kolom berupa nama kolom baru setelah proses transformasi. Disini dapat dilihat dari satu kolom job, akan terbentuk sebanyak 11 kolom baru berdasarkan kategori-kategori yang termuat dalam kolom job. Dapat diperhatikan juga, bahwa kategori pembanding tidak menjadi kolom baru, sehingga kolom baru yang terbentuk dari variabel nominal adalah sebanyak \(C-1\) kolom dengan \(C\) adalah banyaknya kategori.
mod3 <-glm(subscribed=="yes"~job,data=bank_marketing,family=binomial(link = "logit"))tidy_parameters(mod3,ci_method="wald")tidy_parameters(mod3,ci_method="wald",exponentiate = TRUE)- Nilai p-value dari 11 kategori ada yang lebih besar dari \(\alpha=0.05\) dan ada yang kecil. Sehingga kategori-kategori untuk nilai p-value lebih besar dari \(\alpha=0.05\) tidak berpengaruh terhadap puebah responnya.
- Karena ada perbedaan keputusan untuk menolak atau tidak \(H_0\), maka kita agak sulit menyimpulkan apakah variabel
jobberpengaruh atau tidak. Oleh karena itu kita bisa menggunakan Analysis of Deviance untuk menyimpulkan apakahjobberpengaruh atau tidak.
Berikut adalah sintaks untuk menjalankan Analysis of Deviance
anodev <- car::Anova(mod = mod3,type=3)tidy_parameters(anodev)Berdasarkan hasil \(\text{p-value}=0.0001<0.05=\alpha\), dapat disimpulkan bahwa variabel job berpengaruh terhadap subscribed .
Regresi Logistik Berganda
mod4 <- glm(subscribed=="yes"~.,data=bank_marketing,family=binomial(link = "logit"))Pemeriksaan Multikolinearitas
Pemeriksaan multikolinearitas bisa menggunakan VIF.
plot(multicollinearity(x = mod4))+
theme(axis.text.x = element_text(angle = 90))Variable `Component` is not in your data frame :/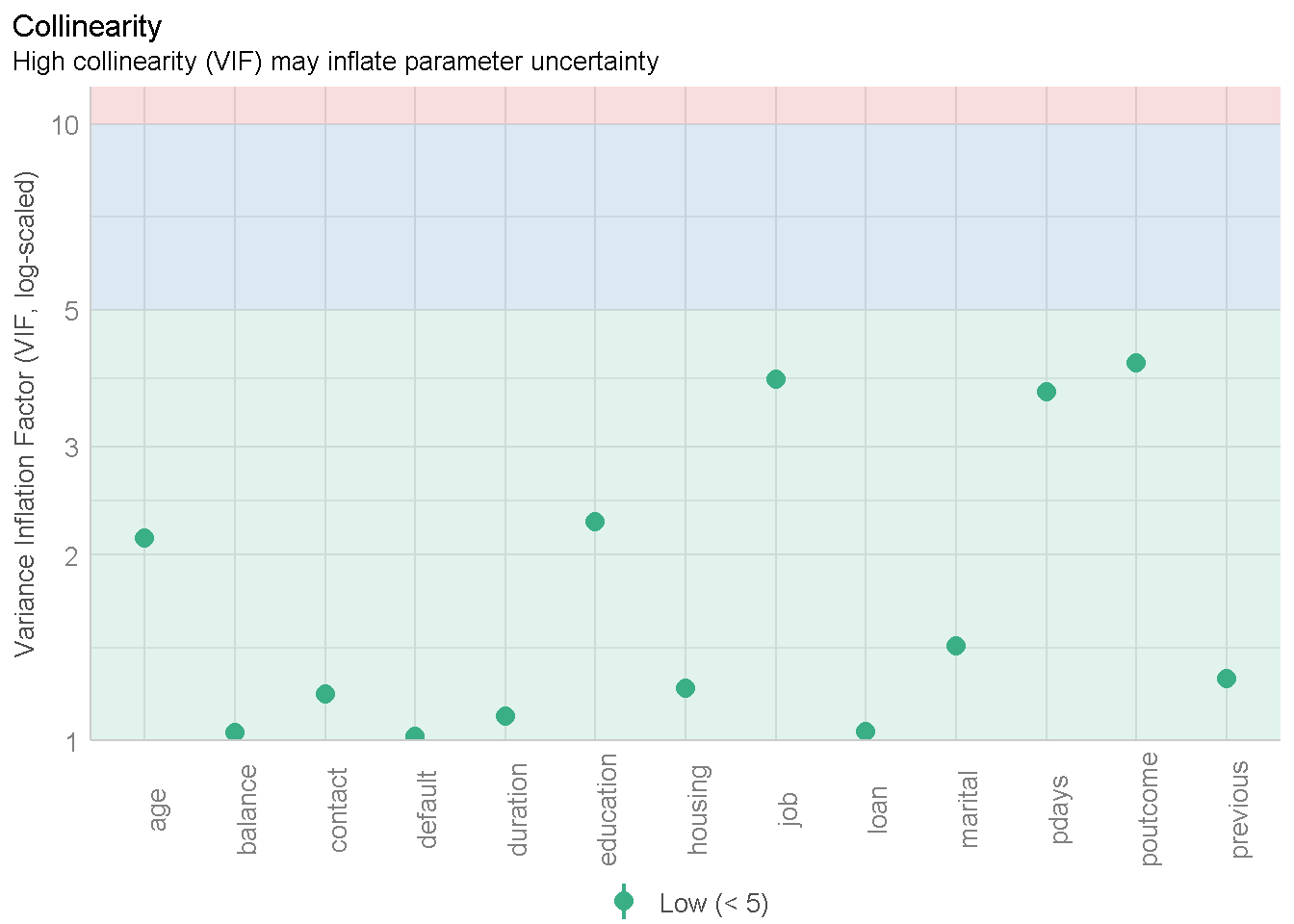
Inferensia Koefisien Regresi Logistik Berganda
tidy_parameters(mod4,conf.int = TRUE,conf.level = 0.95,ci_method="wald",exponentiate = TRUE) %>%
mutate(across(where(is.numeric),function(x) round(x,3) ))Analysis of Deviance Regresi Logistik Berganda
anodev4 <- car::Anova(mod = mod4,type=3)tidy_parameters(anodev4) %>%
mutate(across(where(is.numeric),function(x) round(x,3)))Goodness-of-fits Model
Goodness-of-fits Model biasa menggunakan ukuran-ukuran atau metrik-metrik tertentu yang didasarkan dari log-likehood. Ukuran AICc, BIC, RMSE biasanya digunakan untuk menentukan model terbaik dari beberapa model yang tersedia. Jika hanya satu model saja yang tersedia ukuran ini tidak bisa digunakan. Semakin kecil nila dari AICc, BIC, RMSE maka semakin baik pula modelnya.
Selain itu ada juga ukuran \(R^2\) yang bisa digunakan jika model yang tersedia hanya satu. Nilai \(R^2\) berkisar antara 0 dan 1. Semakin mendekati 1 nilai \(R^2\) semakin baik modelnya.
performance(model = mod4)Kemudian, Goodness-of-fits juga bisa menggunakan uji hipotesis statistik yaitu Likelihood Ratio Test. Secara umum, uji ini membandingkan dua model regresi dan menyimpulkan model mana yang terbaik. Jika kita hanya memliki satu model saja maka model pembandingnya adalah null-model atau model tanpa variabel prediktor dan hanya memuat intercept saja. Hipotesis dari Likelihood Ratio Test adalah sebagai berikut:
\[ \begin{aligned} H_{0}&: \beta_{1}=\beta_{2}=\ldots=\beta_{29}=0 (\text{null-model fit [cocok untuk data}]) &\\ H_{1}&: \exists j, \beta_j \neq 0,j=1,2,\ldots,29 (\text{model yang diusulkan fit [cocok untuk data}]) \end{aligned} \]
The likelihood ratio test statistic \(G\) didefinisikan sebagai:
\[ G = -2 \cdot \log \left(\frac{L_0}{L_1}\right) \]
Di bawah hipotesis nol, \(G\) mengikuti distribusi chi-squared dengan derajat kebebasan yang sama dengan perbedaan jumlah parameter yang diduga pada kedua model. \(L_0\) adalah likelihood dari data pada model nol dan \(L_1\) adalah likelihood dari data pada model yang diusulkan.
Jika likelihood ratio test statistic \(G\) cukup besar, maka kita menolak hipotesis nol dan memilih hipotesis alternatif, yang menunjukkan bahwa parameter tambahan dalam model yang diusulkan secara signifikan meningkatkan fit (kecocokan untuk data). Berikut adalah sintaksnya
test_likelihoodratio(mod4)Only one model was provided, however, at least two are required for
comparison.
Fitting a null-model as reference now.Evaluasi performa prediksi
Pembagian Data
Salah satu metode yang sering digunakan untuk pembagian data yaitu holdout sample. Metode ini membagi amatan pada dateset yang kita miliki menjadi dua bagian yaitu training data dan testing data. Training Data digunakan untuk model “belajar” dari data, sedangkan testing data digunakan untuk evaluasi performa prediksi model. Secara umum, training data harus memiliki amatan yang lebih banyak dibandingkan testing data. Pembagian Banyaknya amatan ini bisanya direpresentasikan dalam bentuk proprosi atau persentase seperti 0.8 atau 80%. Proses pembagian ini biasanya didasarkan pada pengambilan sampel acak (random sampling). Jika variabel respon yang digunakan berupa kategorik disarankan metode pengambilan sampel acak yang digunakan stratified random sampling.
set.seed(123)
holdout_split <- initial_split(data = bank_marketing,
prop = 0.8,
strata ="subscribed")train_data <- training(holdout_split)
test_data <- testing(holdout_split)bank_marketing %>%
mutate(Row=seq(nrow(bank_marketing))) %>%
select(subscribed,Row) %>%
left_join(y = tidy(holdout_split),by = "Row") %>%
count(subscribed,Data) %>%
group_by(subscribed) %>%
mutate(percent=n*100/sum(n),n=NULL) %>%
pivot_wider(id_cols = subscribed,names_from = Data,values_from = percent)Model Training
Model Training dilakukan dengan menggunakan training data yang sudah didapatkan pada proses pembagian data.
mod5 <- glm(subscribed=="yes"~.,data=train_data,family=binomial(link = "logit"))Evaluasi performa prediksi
Berikut adalah sintaks untuk mendapatkan prediksi regresi logistik menggunakan testing data
pred_reglog0 <- predict(mod5,newdata = test_data,type = "response")
head(pred_reglog0) 1 2 3 4 5 6
0.017128630 0.006306462 0.011970850 0.017103661 0.816791011 0.016288098 hasil prediksi dari regresi logistik berupa nilai peluang, semakin besar nilai peluangnya maka semakin besar kemungkinan hasil prediksinya adalah kelas positifnya atau dalam hal ini adalah subscribed=="yes".
Kemudian kita akan satukan hasil prediksi ini dengan kolom subscribed pada data testing dalam bentuk data.frame
pred_reglog <- data.frame(estimate_prob=pred_reglog0,truth=test_data$subscribed)
pred_regloguntuk melakukan evaluasi performa prediksi, maka nilai peluang dari hasil prediksi regresi logistik harus kita konversi menjadi nilai kelas asal yaitu "yes" dan "no". Caranya adalah dengan menentukan suatu threshold tertentu pada nilai peluangnya. Sehingga threshold itulah yang menentukan hasil prediksi mana yang menjadi kelas "yes" atau "no". Berikut adalah sintaksnya
threshold = 0.5
pred_reglog <- pred_reglog %>%
mutate(estimate=if_else(estimate_prob>threshold,"yes","no")) %>%
mutate(estimate=factor(estimate,levels=c("yes","no"))) %>%
# karena positive class dataset adalah no kita perlu rubah dulu ke yes
mutate(truth = factor(truth,levels=c("yes","no")))pred_reglogUmumnya nilai threshold yang digunakan adalah \(0.5\), nilai threshold ini bisa kita ganti berdasarkan subjektivitas pengguna ataupun dengan metode-motode optimalisasi threshold.
Confusion Matrix
Hasil prediksi ini biasanya kita evaluasi dengan suatu nilai metrik tertentu. Sebelum ke metrics tersebut, kita akan mengenal confusion matrix yang menjadi dasar perhitungan metrik-metrik tersebut. Berikut adalah komponen dari confusion matrix

- TRUE POSITIVE (TP): Banyaknya amatan kelas positif yang hasil prediksi modelnya juga kelas positif
- TRUE NEGATIVE (TN): Banyaknya amatan kelas negatif yang hasil prediksi modelnya juga kelas negatif
- FALSE NEGATIVE (FN): Banyaknya amatan kelas negatif yang hasil prediksi modelnya kelas positif
- FALSE POSITIVE (FP): Banyaknya amatan kelas positif yang hasil prediksi modelnya kelas negatif.
Berikut sintaks mengeluarkan confusion matrix.
confussion_matrix <- pred_reglog %>%
conf_mat(truth=truth,estimate=estimate)autoplot(confussion_matrix,type = "heatmap")+
scale_fill_viridis_c(direction = -1,option = "inferno",alpha = 0.6)Scale for fill is already present.
Adding another scale for fill, which will replace the existing scale.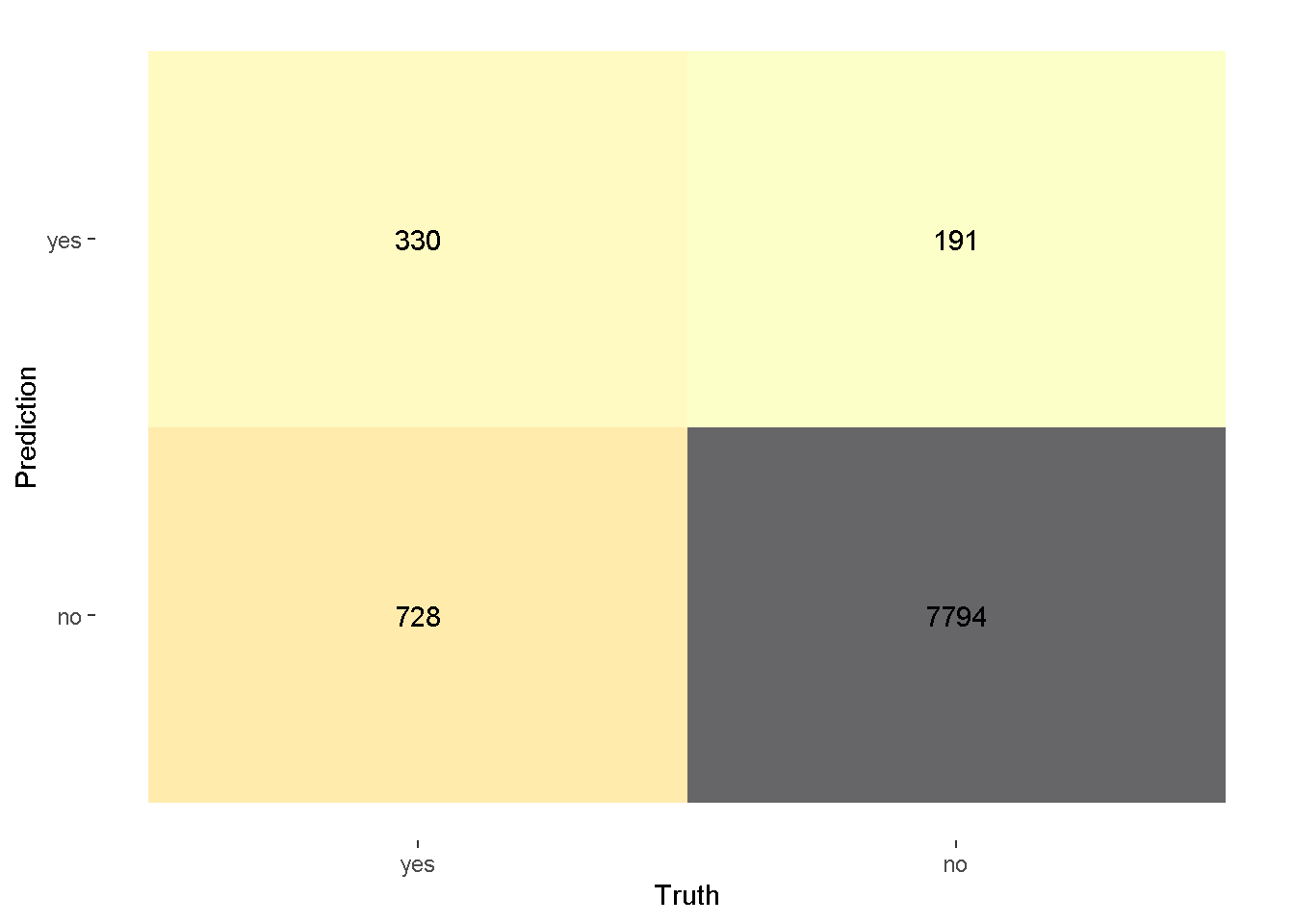
Kemudian berdasarkan TP,TN,FN dan FP dapat dibentuk beberapa metric berikut:
Tentu! Dalam bidang statistika, berbagai metrik digunakan untuk mengevaluasi kinerja model klasifikasi berdasarkan matriks kebingungannya. Matriks kebingungan adalah tabel yang menggambarkan kinerja model klasifikasi. Ini menyajikan ringkasan dari prediksi model pada sekelompok data di mana nilai sejati diketahui. Matriks ini memiliki empat entri mungkin: true positives (TP), true negatives (TN), false positives (FP), dan false negatives (FN).
Berikut adalah beberapa metrik umum yang berasal dari matriks kebingungan:
- Accuracy (ACC):
Accuracy(Akurasi) adalah ukuran banyaknya hasil prediksi model yang benar dari keseluruhan hasil prediksi model.
Formula:
\[ \text{Accuracy} = \frac{{TP + TN}}{{TP + TN + FP + FN}} \]
- Precision (juga disebut Positive Predictive Value):
Precision (Presisi) adalah proporsi prediksi kelas positif yang benar dari total kelas positif yang diprediksi.
Formula:
\[ \text{Precision} = \frac{{TP}}{{TP + FP}} \]
- Recall (juga disebut Sensitivity, Hit Rate, atau True Positive Rate):
Recall adalah proporsi kelas positif yang diprediksi benar dari total kelas positif yang sebenarnya.
Formula:
\[ \text{Recall} = \frac{{TP}}{{TP + FN}} \]
- F1-Score:
F1-Score adalah rata-rata harmonik dari presisi dan recall. Metric ini mempertimbangkan keseimbangan antara precision dan recall.
Formula:
\[ \text{F}1 = 2 \times \frac{{\text{Precision} \times \text{Recall}}}{{\text{Precision} + \text{Recall}}} \]
- Specificity (juga disebut True Negative Rate)):
Specificity mengukur proporsi kelas negatif yang diprediksi benar dari total kelas negatif yang sebenarnya.
Formula:
\[ \text{Specificity} = \frac{{TN}}{{TN + FP}} \]
- False Positive Rate (FPR):
FPR mengukur proporsi FALSE POSITIVE dari total kelas negatif sebenarnya.
Formula:
\[ FPR = 1 - \text{Specificity} = \frac{{FP}}{{TN + FP}} \]
- False Negative Rate (FNR):
FNR mengukur proporsi FALSE NEGATIVE dari total kelas positif sebenarnya.
Formula:
\[ FNR = \frac{{FN}}{{TP + FN}} \]
- Koefisien Korelasi Matthews (MCC):
MCC adalah ukuran kualitas klasifikasi biner, mempertimbangkan keempat elemen confusion matrix.
Formula:
\[ MCC = \frac{{TP \times TN - FP \times FN}}{{\sqrt{{(TP + FP)(TP + FN)(TN + FP)(TN + FN)}}}} \]
- Balanced Accuracy:
- Balanced Accuracy adalah metrik evaluasi yang berguna ketika dataset memiliki ketimpangan (imbalance) di antara kelas-kelas yang berbeda. Metrik ini memberikan akurasi yang seimbang antara kelas mayoritas dan minoritas.
Formula:
\[ \text{Balanced Accuracy} = \frac{{\text{Specificity} + \text{Sensitivity}}}{{2}} \]
metrik-metrik ini bisa dikeluarkan dengan sintaks berikut:
confussion_matrix %>%
summary()atau kita bisa mengeluarkan salah satu saja seperti berikut
pred_reglog %>%
accuracy(estimate = estimate,truth = truth)atau kita bisa mengeluarkan beberapa
multi_metric <- metric_set(accuracy,sensitivity,specificity,bal_accuracy,mcc,f_meas)
pred_reglog %>%
multi_metric(estimate = estimate,truth = truth)Kurva ROC
Evaluasi performa prediksi juga bisa didapatkan dengan menggunakan nilai peluang hasil prediksi yang didapatkan dari regresi logistik. Nilai peluang tersebut pada langkah sebelumnya disimpan dalam kolom estimate_prob.
pred_reglogSalah satu alat yang digunakan untuk melakukan evaluasi performa prediksi berdasarkan prediksi peluang adalah kurva ROC. Berikut adalah sintaksnya
kurva_roc <- pred_reglog %>%
roc_curve(truth = truth,estimate_prob)
kurva_roc autoplot(kurva_roc)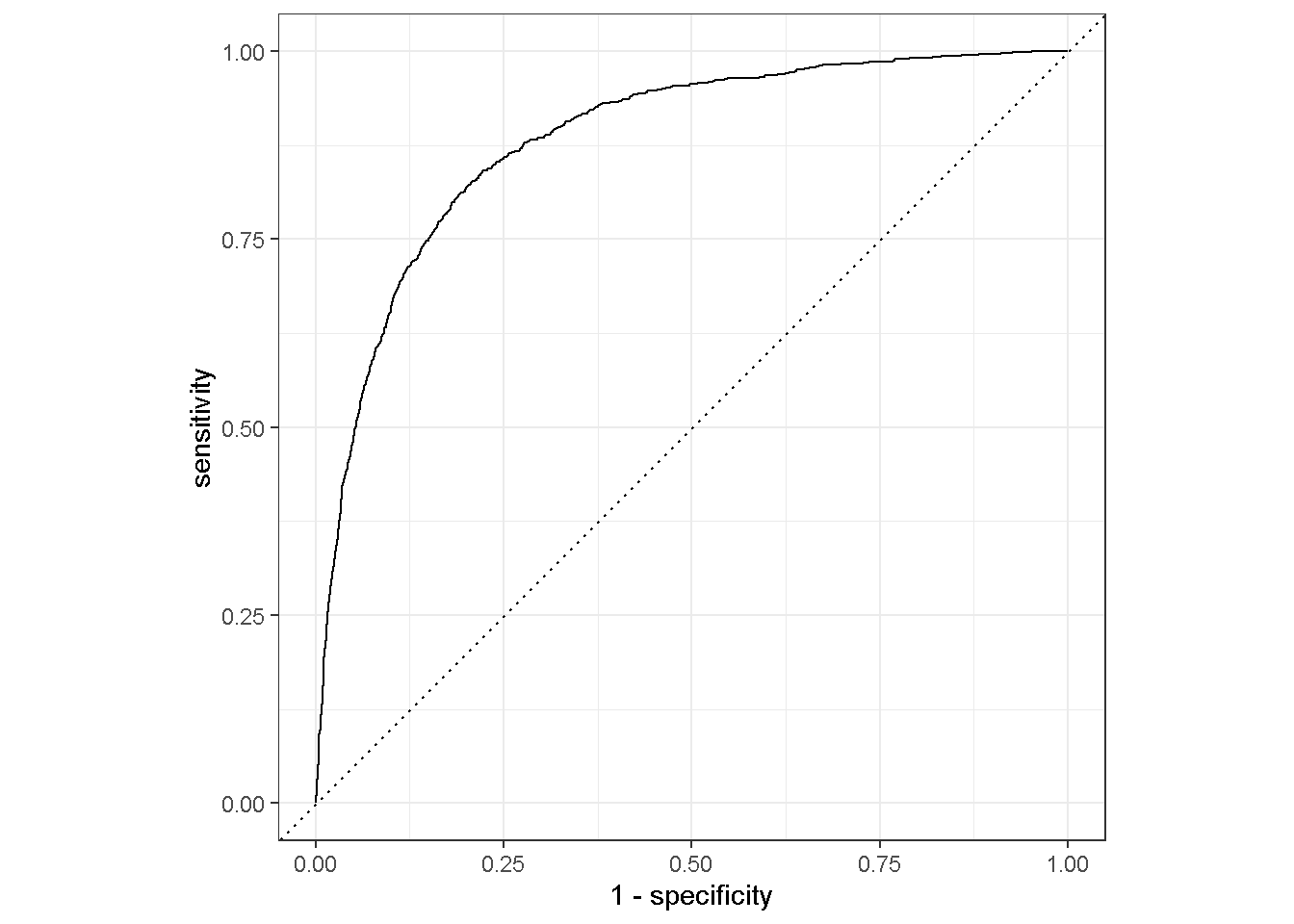
Berdasarkan dua output diatas, kita bisa melihat bahwa kurva ROC dibentuk berdasarkan metrik sensitivity dan specificity yang dihitung dari berbagai macam kemungkinan threshold. Oleh karena itu, kurva ROC ini juga sering digunakan untuk mendapatkan threshold optimal berdasarkan sensitivity dan specificity.
Kurva ROC ini biasanya digunakan untuk menentukan model dengan performa prediksi terbaik. Namun, pada ilustrasi ini kita hanya menggunakan satu model sehingga kurva ROC ini kurang bisa digunakan. Tetapi, terdapat metrik yang berbasiskan kurva roc yang bisa digunakan tanpa membandingkan dengan model lain yaitu AREA Under Curve (AUC).
pred_reglog %>%
roc_auc(truth = truth,estimate_prob)Threshold Optimal
Selanjutnya kita akan mencoba mendapatkan threshold optimal berdasarkan sensitivity dan specificity menggunakan Youden’s J statistic yang didefinisikan sebagai berikut
\[ \text{Youden's J statistic} = \text{sensitivity} + \text{specificity}-1 \]
Semakin mendekati 1 nilainya maka semakin baik thresholdnya dan semakin nilainya mendekati 0 semakin buruk thresholdnya. Jika kita terapkan pada sintaks adalah sebagai berikut.
kurva_roc %>%
mutate(youden_index=sensitivity+specificity-1)kemudian karena kita mencari Youden’s J statistic yang mendekati satu berarti sama saja kita mencari nilai threshold yang Youden’s J statistic paling maksimum. Kita bisa mendapatkan nilai maksimum ini dengan bantuan fungsi slice_max
optimal_thresh <- kurva_roc %>%
mutate(youden_index=sensitivity+specificity-1) %>%
slice_max(order_by = youden_index)
optimal_threshKemudian hasil prediksi dengan threshold optimal bisa didapatkan dengan sintaks berikut
pred_reglog2 <- data.frame(estimate_prob=pred_reglog0,truth=test_data$subscribed)
threshold2 = optimal_thresh %>% pull(.threshold)
pred_reglog2 <- pred_reglog2 %>%
mutate(estimate=if_else(estimate_prob>threshold2,"yes","no")) %>%
mutate(estimate=factor(estimate,levels=c("yes","no"))) %>%
# karena positive class dataset adalah no kita perlu rubah dulu ke yes
mutate(truth = factor(truth,levels=c("yes","no")))
pred_reglog2Kemudian jika kita bandingkan antara threshold 0.5 dengan threshold optimal pada beberapa metric maka hasilnya adalah sebagai berikut
res_metric2 <- pred_reglog2 %>%
multi_metric(truth = truth,estimate = estimate) %>%
mutate(threshold=threshold2) %>%
relocate(threshold,.after = .metric)
res_metric <- pred_reglog %>%
multi_metric(truth = truth,estimate = estimate) %>%
mutate(threshold=threshold) %>%
relocate(threshold,.after = .metric)res_metric2 %>%
bind_rows(res_metric) %>%
select(-.estimator) %>%
pivot_wider(id_cols = .metric,names_from = threshold,
names_prefix ="thres=",
values_from = .estimate)Prediksi Data Baru
untuk mengilustrasikan prediksi pada data baru, kita akan membuat suatu data baru “buatan” dengan mengambil sampel acak dari data bank_marketing. Data baru bisanya tidak memuat variabel response sehingga kita akan hilangkan kolom subscribed.
set.seed(123)
data_baru <- bank_marketing %>%
slice_sample(n = 10) %>%
select(-subscribed)
data_barupred_data_baru <- predict(mod4,newdata = data_baru,type = "response")threshold2[1] 0.1037991pred_data_baru_df <- data.frame(estimate=pred_data_baru) %>%
mutate(estimate=if_else(estimate>threshold2,"yes","no")) %>%
mutate(estimate=factor(estimate,levels=c("no","yes")))
pred_data_baru_df