install.packages("tidyverse")
install.packages("broom")
install.packages("performance")
install.packages("see")
install.packages("fbasics")
install.packages("sjplot")
install.packages("ggpubr")
install.packages("DescTools")Analisis Faktorial RAL dengan R
Install package berikut jika belum ada
library(tidyverse)
library(performance)
library(see)
library(sjPlot)
library(broom)
library(ggpubr)
library(DescTools)
library(fBasics)Data
Dari percobaan ini ingin diketahui apakah jenis material dan suhu mempengaruhi daya tahan baterai (dalam jam) ? Apakah jenis material tertentu cocok untuk suhu tertentu? Dari percobaan tersebut diperoleh data daya tahan baterai sebagai berikut:
| Material | Suhu | DayaTahan |
|---|---|---|
| A | 15 | 130 |
| A | 70 | 34 |
| A | 125 | 20 |
| A | 15 | 74 |
| A | 70 | 80 |
| A | 125 | 82 |
| A | 15 | 155 |
| A | 70 | 40 |
| A | 125 | 70 |
| A | 15 | 180 |
| A | 70 | 75 |
| A | 125 | 58 |
| B | 15 | 150 |
| B | 70 | 136 |
| B | 125 | 25 |
| B | 15 | 159 |
| B | 70 | 106 |
| B | 125 | 70 |
| B | 15 | 188 |
| B | 70 | 122 |
| B | 125 | 58 |
| B | 15 | 126 |
| B | 70 | 115 |
| B | 125 | 45 |
| C | 15 | 138 |
| C | 70 | 174 |
| C | 125 | 96 |
| C | 15 | 168 |
| C | 70 | 150 |
| C | 125 | 82 |
| C | 15 | 110 |
| C | 70 | 120 |
| C | 125 | 104 |
| C | 15 | 160 |
| C | 70 | 139 |
| C | 125 | 60 |
Import Data ke dalam R
Untuk import data ke R kita bisa langsung menuliskan data nya di R dengan sintaks seperti dibawah ini
baterai <- read.table(header = T,stringsAsFactors = T,text =
"Material Suhu DayaTahan
A 15 130
A 70 34
A 125 20
A 15 74
A 70 80
A 125 82
A 15 155
A 70 40
A 125 70
A 15 180
A 70 75
A 125 58
B 15 150
B 70 136
B 125 25
B 15 159
B 70 106
B 125 70
B 15 188
B 70 122
B 125 58
B 15 126
B 70 115
B 125 45
C 15 138
C 70 174
C 125 96
C 15 168
C 70 150
C 125 82
C 15 110
C 70 120
C 125 104
C 15 160
C 70 139
C 125 60
")Melihat data sekilas dengan fungsi glimpse dari package dplyr
glimpse(baterai)Rows: 36
Columns: 3
$ Material <fct> A, A, A, A, A, A, A, A, A, A, A, A, B, B, B, B, B, B, B, B, …
$ Suhu <int> 15, 70, 125, 15, 70, 125, 15, 70, 125, 15, 70, 125, 15, 70, …
$ DayaTahan <int> 130, 34, 20, 74, 80, 82, 155, 40, 70, 180, 75, 58, 150, 136,…baterai <- baterai %>%
#merubah kolom suhu menjadi factor(kategorik)
mutate(Suhu=as.factor(Suhu))
glimpse(baterai)Rows: 36
Columns: 3
$ Material <fct> A, A, A, A, A, A, A, A, A, A, A, A, B, B, B, B, B, B, B, B, …
$ Suhu <fct> 15, 70, 125, 15, 70, 125, 15, 70, 125, 15, 70, 125, 15, 70, …
$ DayaTahan <int> 130, 34, 20, 74, 80, 82, 155, 40, 70, 180, 75, 58, 150, 136,…Analysis of Variance (ANOVA)
Hipotesis untuk material baterai
\[ \begin{aligned} H_{0} &: \text{jenis material baterai tidak mempengaruhi Daya Tahan Baterai} \\ H_{1} &: \text{terdapat minimal satu jenis material baterai yang mempengaruhi Daya Tahan Baterai} \end{aligned} \]
Hipotesis untuk Suhu Baterai
\[ \begin{aligned} H_{0} &: \text{jenis material baterai tidak mempengaruhi Daya Tahan Baterai} \\ H_{1} &: \text{terdapat minimal satu jenis material baterai yang mempengaruhi Daya Tahan Baterai} \end{aligned} \]
Hipotesis untuk Interaksi Daya Tahan dan Suhu Baterai
\[ \begin{aligned} H_{0} &: \text{interaksi antara material dan suhu tidak berpengaruh terhadap daya tahan baterai} \\ H_{1} &: \text{interaksi antara material dan suhu berpengaruh terhadap daya tahan baterai} \end{aligned} \]
anova_bat <- aov(DayaTahan~Material+Suhu+Material:Suhu,data=baterai)Catatan:
Material:Suhumenandakan interaksi antara suhu dan material
tidy(anova_bat) %>%
mutate(p.value=round(p.value,3))# A tibble: 4 × 6
term df sumsq meansq statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Material 2 10684. 5342. 7.91 0.002
2 Suhu 2 39119. 19559. 29.0 0
3 Material:Suhu 4 9614. 2403. 3.56 0.019
4 Residuals 27 18231. 675. NA NA Saat \(\alpha=0.05\)
Interaksi antara Material dan Suhu
karena p-value yang dihasilkan dari uji ANOVA kurang dari 0.05 maka \(H_{0}\) ditolak atau dengan kata lain cukup bukti untuk mengatakan bahwa interaksi antara material dan suhu berpengaruh terhadap daya tahan baterai
Karena Interaksi antara faktor material dan suhu signifikan (\(H_{0}\) ditolak) maka kita bisa mengabaikan pengujian hipotesis untuk masing-masing faktor material dan suhu baterai.
Langkah selajutnya kita bisa melihat plot interaksi sebagai berikut:
Grafik Interaksi
plot_model(anova_bat,type = "int")+
geom_line()+
theme_lucid()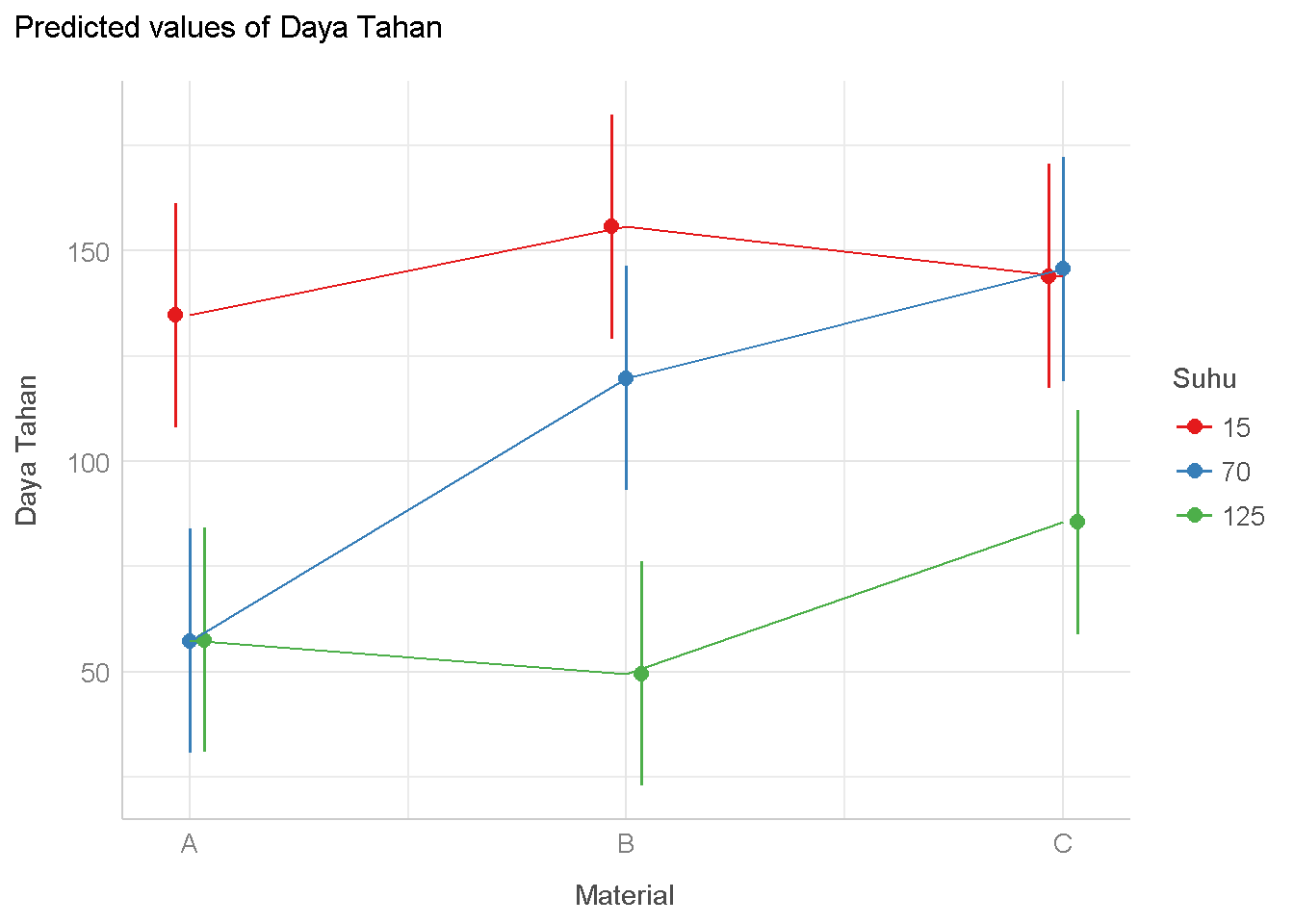
Saat \(\alpha=0.01\)
Interaksi antara Material dan Suhu
karena p-value yang dihasilkan dari uji ANOVA lebih dari 0.01 maka \(H_{0}\) tidak ditolak atau dengan kata lain Interaksi antara material dan suhu tidak berpengaruh terhadap daya tahan baterai
Karena Interaksi antara faktor material dan suhu tidak signifikan (\(H_{0}\) tidak ditolak) pada \(\alpha=0.01\) maka kita melakukan pengujian hipotesis untuk masing-masing faktor material dan suhu baterai.
Material
karena p-value yang dihasilkan dari uji ANOVA kurang dari 0.01 maka \(H_{0}\) ditolak atau dengan kata lain terdapat minimal satu jenis material baterai yang mempengaruhi Daya Tahan Baterai
Suhu
karena p-value yang dihasilkan dari uji ANOVA kurang dari 0.01 maka \(H_{0}\) ditolak atau dengan kata lain terdapat minimal satu temperatur suhu baterai yang mempengaruhi Daya Tahan Baterai
Uji Lanjut (Multiple Comparison)
Faktor Material dan Suhu material signifikan pada \(\alpha=0.01\) sehingga kita bisa menggunakan Uji lanjut untuk menyelidiki lebih lanjut.
Sebelum melakukan uji lanjut, kita akan membuat objek baru (anova_bat2) di R untuk menyimpan hasil ANOVA tanpa interaksi.
anova_bat2 <- aov(DayaTahan~Material+Suhu,data=baterai)Hipotesis Uji lanjut
\[ \begin{aligned} H_{0} &: \mu_{i}-\mu_{j}=0 \space \text{untuk} \space i \neq j \\ H_{1} &: \mu_{i}-\mu_{j} \neq 0 \space \text{untuk} \space i \neq j \end{aligned} \]
atau
\[ \begin{aligned} H_{0} &: \text{tidak ada perbedaan rata-rata Daya Tahan Baterai material/suhu ke-i dan ke-j} \\ H_{1} &: \text{Ada perbedaan rata-rata Daya Tahan Baterai material/suhu ke-i dan ke-j} \end{aligned} \]
dengan \(\mu_{i}\) adalah rata-rata material/suhu baterai ke-i untuk \(i=1,2,3\)
Honest Significant Difference (HSD) atau Tukey Test
PostHocTest(anova_bat2,method="hsd")
Posthoc multiple comparisons of means : Tukey HSD
95% family-wise confidence level
$Material
diff lwr.ci upr.ci pval
B-A 25.16667 -4.946637 55.27997 0.1157
C-A 41.91667 11.803363 72.02997 0.0048 **
C-B 16.75000 -13.363303 46.86330 0.3692
$Suhu
diff lwr.ci upr.ci pval
70-15 -37.25000 -67.36330 -7.136697 0.0128 *
125-15 -80.66667 -110.77997 -50.553363 6.8e-07 ***
125-70 -43.41667 -73.52997 -13.303363 0.0035 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Material
Berdasarkan HSD test, p-value B-A dan C-B lebih besar dari 0.05, artinya tidak ada perbedaan rata-rata Daya Tahan Baterai material A dan B; B dan C. Sementara itu, p-value C-A lebih kecil dari 0.05, artinya ada perbedaan rata-rata Daya Tahan Baterai material A dan C.
Suhu
Berdasarkan HSD test, p-value 70-15, 125-15 dan 125-70 lebih kecil dari 0.05, artinya ada perbedaan rata-rata Daya Tahan Baterai Suhu 15 dan 70; 15 dan 125;70 dan 125.
Fisher Least Significant Difference (LSD)
PostHocTest(anova_bat2,method="lsd")
Posthoc multiple comparisons of means : Fisher LSD
95% family-wise confidence level
$Material
diff lwr.ci upr.ci pval
B-A 25.16667 0.2126748 50.12066 0.0482 *
C-A 41.91667 16.9626748 66.87066 0.0017 **
C-B 16.75000 -8.2039919 41.70399 0.1808
$Suhu
diff lwr.ci upr.ci pval
70-15 -37.25000 -62.20399 -12.29601 0.0047 **
125-15 -80.66667 -105.62066 -55.71267 2.3e-07 ***
125-70 -43.41667 -68.37066 -18.46267 0.0013 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Material
Berdasarkan LSD test, p-value B-A dan C-A lebih kecil dari 0.05, artinya ada perbedaan rata-rata Daya Tahan Baterai material A dan B; a dan C. Sementara itu, p-value C-B lebih besar dari 0.05, artinya tidak ada perbedaan rata-rata Daya Tahan Baterai material B dan C.
Suhu
Berdasarkan LSD test, p-value 70-15, 125-15 dan 125-70 lebih kecil dari 0.05, artinya ada perbedaan rata-rata Daya Tahan Baterai Suhu 15 dan 70; 15 dan 125;70 dan 125.
Bonferroni Test
PostHocTest(anova_bat2,method="bonf")
Posthoc multiple comparisons of means : Bonferroni
95% family-wise confidence level
$Material
diff lwr.ci upr.ci pval
B-A 25.16667 -5.799887 56.13322 0.1446
C-A 41.91667 10.950113 72.88322 0.0052 **
C-B 16.75000 -14.216554 47.71655 0.5425
$Suhu
diff lwr.ci upr.ci pval
70-15 -37.25000 -68.21655 -6.283446 0.0142 *
125-15 -80.66667 -111.63322 -49.700113 6.9e-07 ***
125-70 -43.41667 -74.38322 -12.450113 0.0038 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Material
Berdasarkan Bonferroni test, p-value B-A dan C-B lebih besar dari 0.05, artinya tidak ada perbedaan rata-rata Daya Tahan Baterai material A dan B; B dan C. Sementara itu, p-value C-A lebih kecil dari 0.05, artinya ada perbedaan rata-rata Daya Tahan Baterai material A dan C.
Suhu
Berdasarkan Bonferroni test, p-value 70-15, 125-15 dan 125-70 lebih kecil dari 0.05, artinya ada perbedaan rata-rata Daya Tahan Baterai Suhu 15 dan 70; 15 dan 125;70 dan 125.
Duncan Test
PostHocTest(anova_bat2,method="duncan")
Posthoc multiple comparisons of means : Duncan's new multiple range test
95% family-wise confidence level
$Material
diff lwr.ci upr.ci pval
B-A 25.16667 0.2126748 50.12066 0.0482 *
C-A 41.91667 15.6907301 68.14260 0.0024 **
C-B 16.75000 -8.2039919 41.70399 0.1808
$Suhu
diff lwr.ci upr.ci pval
70-15 -37.25000 -62.20399 -12.29601 0.0047 **
125-15 -80.66667 -106.89260 -54.44073 3.4e-07 ***
125-70 -43.41667 -68.37066 -18.46267 0.0013 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Material
Berdasarkan Duncan test, p-value B-A dan C-A lebih kecil dari 0.05, artinya ada perbedaan rata-rata Daya Tahan Baterai material A dan B; A dan C. Sementara itu, p-value C-B lebih besar dari 0.05, artinya tidak ada perbedaan rata-rata Daya Tahan Baterai material B dan C.
Suhu
Berdasarkan Duncan test, p-value 70-15, 125-15 dan 125-70 lebih kecil dari 0.05, artinya ada perbedaan rata-rata Daya Tahan Baterai Suhu 15 dan 70; 15 dan 125;70 dan 125.
Pemeriksaan Asumsi ANOVA
Pemeriksaan asumsi ANOVA dilakukan pada residual nya. Untuk mengeluarkan residualnya bisa menggunakan sintaks dibawah ini
aug1 <- augment(anova_bat)
aug1# A tibble: 36 × 9
DayaTahan Material Suhu .fitted .resid .hat .sigma .cooksd .std.resid
<int> <fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 130 A 15 135. -4.75 0.250 26.5 0.00165 -0.211
2 34 A 70 57.3 -23.3 0.250 26.0 0.0395 -1.03
3 20 A 125 57.5 -37.5 0.250 25.1 0.103 -1.67
4 74 A 15 135. -60.7 0.250 22.6 0.270 -2.70
5 80 A 70 57.3 22.7 0.250 26.0 0.0379 1.01
6 82 A 125 57.5 24.5 0.250 25.9 0.0439 1.09
7 155 A 15 135. 20.3 0.250 26.1 0.0300 0.900
8 40 A 70 57.3 -17.3 0.25 26.2 0.0218 -0.767
9 70 A 125 57.5 12.5 0.25 26.3 0.0114 0.555
10 180 A 15 135. 45.3 0.250 24.4 0.150 2.01
# ℹ 26 more rowsNormalitas (Residual Menyebar Normal)
Pemeriksaan Normalitas bisa dilakukan dengan menggunakan grafik atau uji hipotesis.
Grafik
untuk menampilkan grafik dibawah ini terlebih dahulu harus memanggil package performance dan see
plot(check_normality(x = anova_bat),type="qq")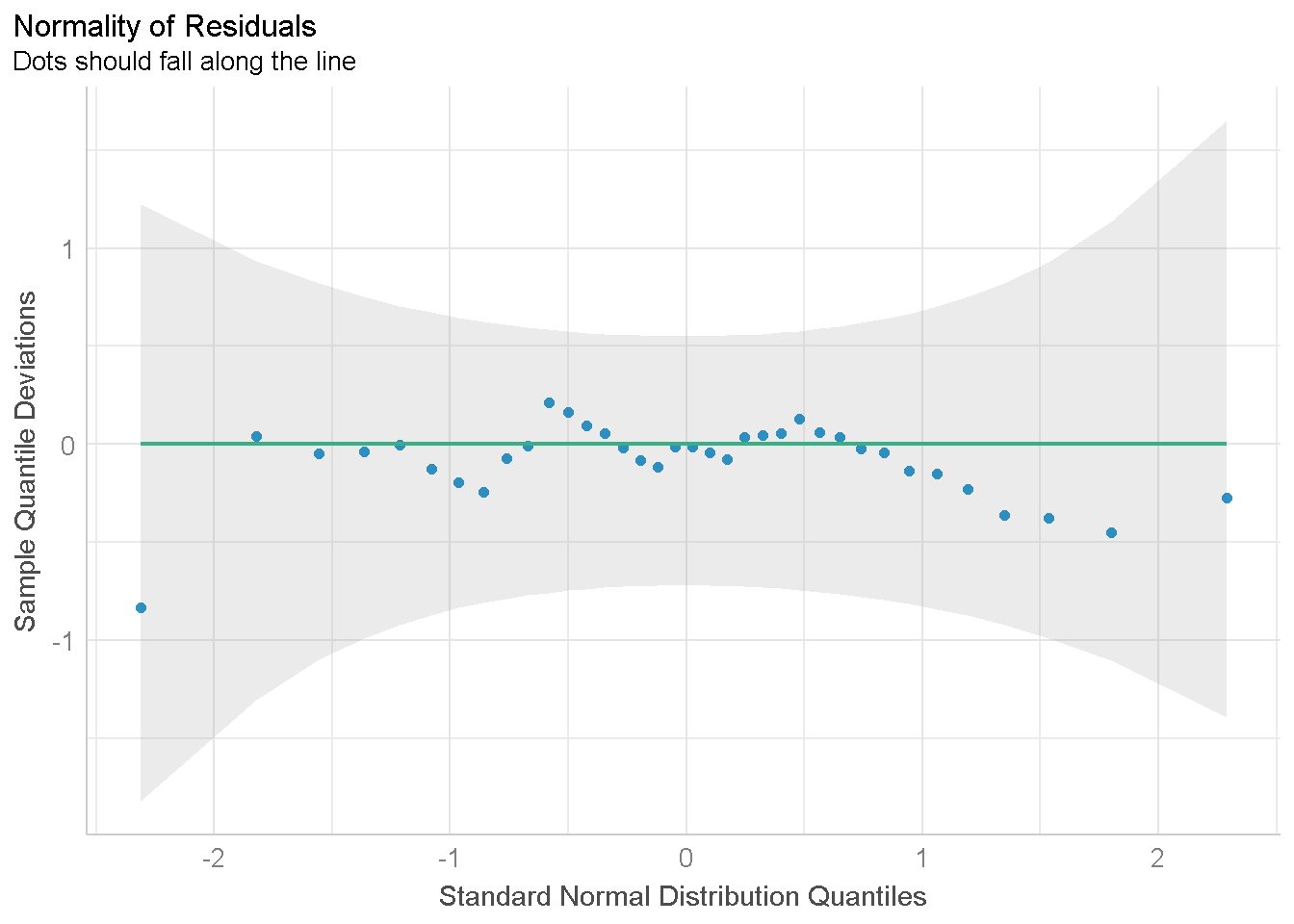
Dari grafik ini, titik-titik residual yang mengikuti pola garis dan berada di dalam daerah selang kepercayaan maka diduga bahwa asumsi normalitas dipenuhi.
Uji Hipotesis
Hipotesis yang diuji untuk pemeriksaan normalitas adalah
\[ \begin{aligned} H_{0} &: \text{galat menyebar normal} \\ H_{1} &: \text{galat tidak menyebar normal} \end{aligned} \]
Uji Normalitas bisa dilakukan dengan beberapa metode pengujian. Untuk itu, akan dibuat fungsi R agar dapat menjalankan metode-metode pengujian tersebut. Fungsi R ini tidak perlu dipahami secara serius karena dapat digunakan untuk berbagai kondisi data. Fungsi R buatan ini sangat bergantung pada package fbasics
## fungsi R buatan
normal_test <- function(data,variable){
ad_stat <- adTest(
data %>%
pull(variable)
)@test$statistic
ks_stat <- ksnormTest(
data %>%
pull(variable)
)@test$statistic
jb_stat <- jarqueberaTest(
data %>%
pull(variable)
)@test$statistic
shapiro_stat <- shapiroTest(
data %>%
pull(variable)
)@test$statistic
ad_p.value <- adTest(
data %>%
pull(variable)
)@test$p.value
ks_p.value <- ksnormTest(
data %>%
pull(variable)
)@test$p.value
jb_p.value <- jarqueberaTest(
data %>%
pull(variable)
)@test$p.value
shapiro_p.value <- shapiroTest(
data %>%
pull(variable)
)@test$p.value
all_stats <- data.frame(statistic=c(ad_stat, ks_stat[1],
jb_stat,
shapiro_stat),
p.value=c(
ad_p.value, ks_p.value[1],
jb_p.value,
shapiro_p.value
)) %>%
mutate(across(where(is.numeric),~ round(.x,3))) %>%
mutate(name=c("Anderson-Darling",
"Kolmogorov-Smirnov",
"Shapiro-Wilk",
"Jarque-Bera")) %>%
relocate(name)
rownames(all_stats) <- NULL
return(all_stats)
}normal_test(data = aug1,
variable = ".resid") name statistic p.value
1 Anderson-Darling 0.340 0.478
2 Kolmogorov-Smirnov 0.488 0.000
3 Shapiro-Wilk 1.192 0.551
4 Jarque-Bera 0.976 0.612karena p-value yang dihasilkan dari 3 uji normalitas lebih dari 0.05 maka \(H_{0}\) tidak ditolak atau dengan kata lain galat menyebar normal
Homogenitas
Pemeriksaan Homogenitas bisa dilakukan dengan menggunakan grafik atau uji hipotesis.
Grafik
untuk menampilkan grafik dibawah ini menggunakan package ggpubr
ggscatter(data = aug1,
x=".fitted",
y=".resid")+
geom_hline(aes(yintercept=0)) +
theme_lucid()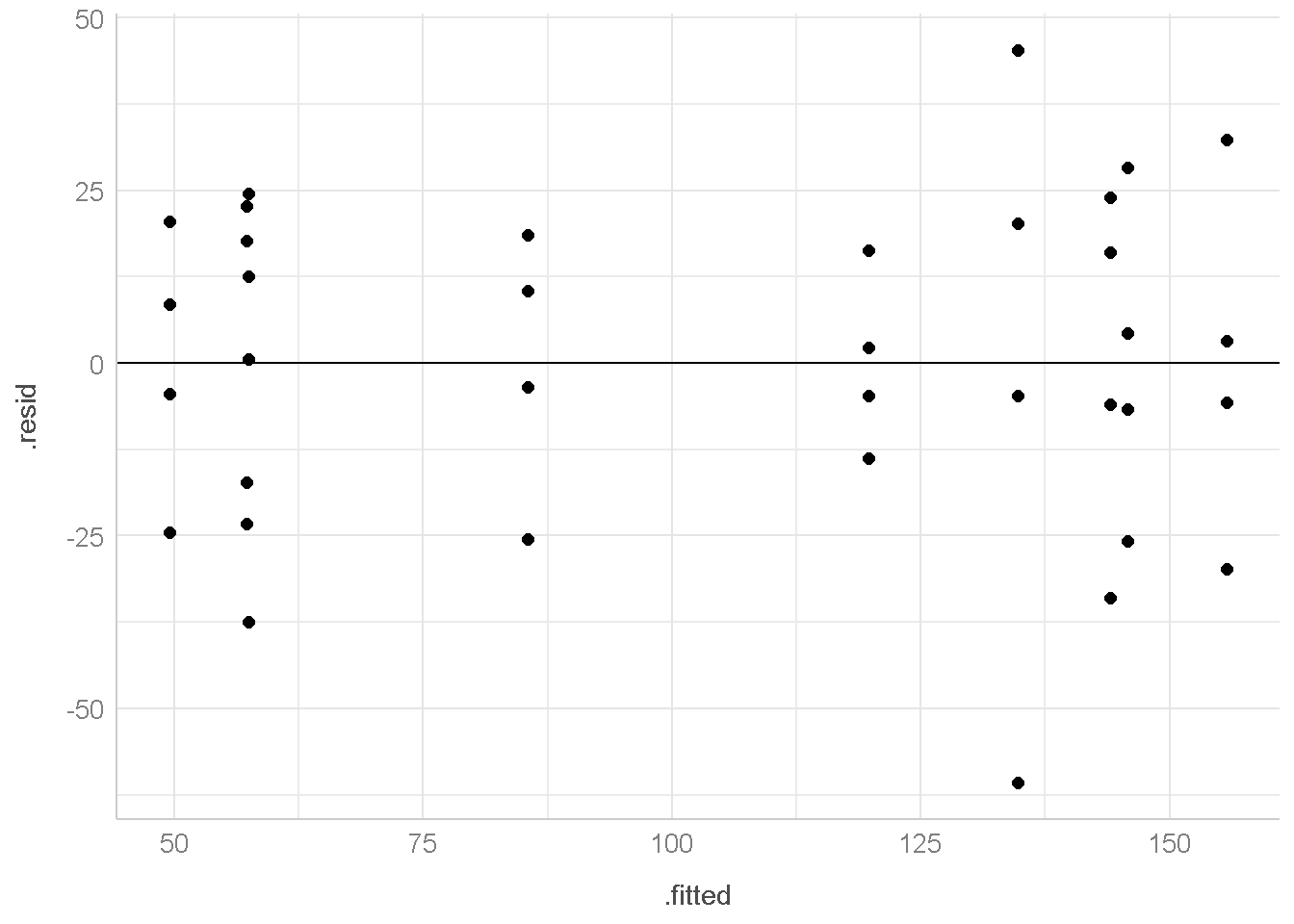
Dari grafik ini, tidak terdapat pola berbentuk corong (funnel shape) maka diduga bahwa asumsi homogenitas terpenuhi.
Uji Hipotesis
Hipotesis yang diuji untuk pemeriksaan homogenitas adalah
\[ \begin{aligned} H_{0} &: \text{ragam homogen antar perlakukan} \\ H_{1} &: \text{ragam tidak homogen antar perlakuan} \end{aligned} \]
Uji Homogenitas bisa dilakukan dengan beberapa metode pengujian dibawah ini
# Bartlett (asumsi residual menyebar normal)
check_homogeneity(anova_bat,method="bartlett")OK: There is not clear evidence for different variances across groups (Bartlett Test, p = 0.732).# Fligner (merupakan uji nonparametrik)
check_homogeneity(anova_bat,method="fligner")OK: There is not clear evidence for different variances across groups (Fligner-Killeen Test, p = 0.684).karena p-value yang dihasilkan dari uji homogenitas lebih dari 0.05 maka \(H_{0}\) tidak ditolak atau dengan kata lain ragam homogen antar perlakukan
Independent
Grafik
Pemeriksaan Independent bisa dilakukan dengan menggunakan grafik.
untuk menampilkan grafik dibawah ini menggunakan package ggpubr
aug1 %>%
mutate(order=seq(nrow(aug1))) %>%
ggscatter(x="order",y=".resid")+
theme_lucid()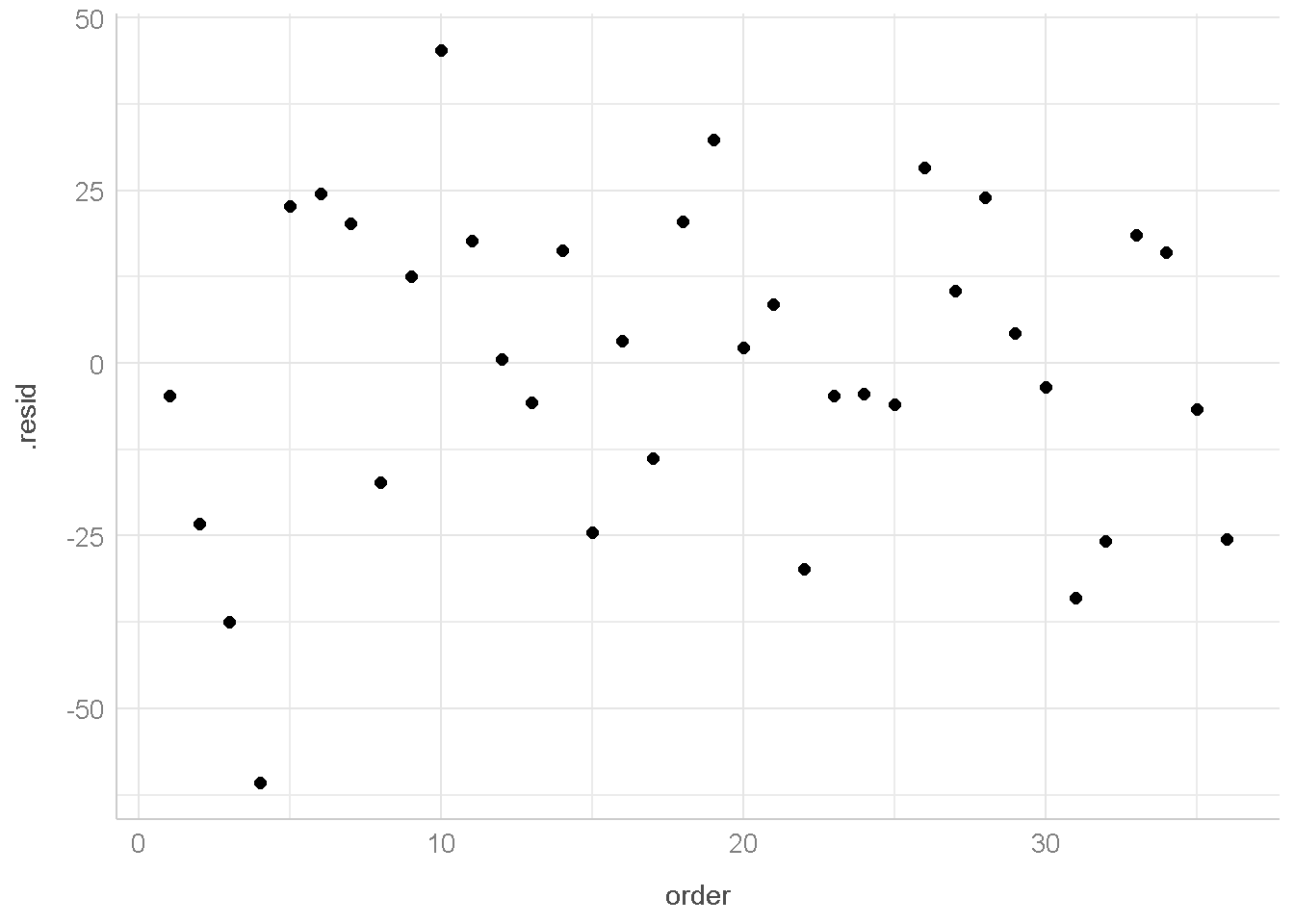
Dari grafik ini, tidak terbentuk pola tertentu (misal pola linear) maka diduga bahwa asumsi Independent dipenuhi.